|
There are many practical situations where we try to simplify a problem by transforming it. We investigate how various regions in the plane are transformed by elementary analytic functions. You may find the following website helpful: http://www.malilla.supereva.it/Pages/Fractals/Cmapper/cm.html 1. w = f(z) = z + c (c = (c1, c2) Each z = (x, y) maps to w = (x + c1, y + c2). 2. Let b = | b | cis If z = r cis Thus we have a rotation about O through The general linear function is the mapping w = f(z) = bz + c. z
Let w = f(z) = z 2. Then if z = r cis
We note that in general, the mapping w = f(z) = z2 will not be 1–1. For example, the points Let us now write w = f(z) = z 2 in cartesian coordinates. Setting w = u + iv, z = x + iy, we obtain u + iv = (x2 – y2) + 2xyi. That is, (x, y) So z-points on the hyperbola x2 – y2 = k map to points on the straight line u = k.
The mapping w = f(z) =1/z (equivalently z = 1/w) sets up a 1–1 correspondence between points in the z- and w-planes excluding z = 0, w = 0. In polar coordinates w = 1/z becomes This transformation is the product of two simpler transformations: z = r cis – inversion in the unit circle Notes 2. Under w = 1/z, (and under inversion),
Question What is the effect of f(z) = 1/z on more general lines and circles? Expressing w = f(z) = 1/z in terms of cartesian coordinates, we obtain
Thus
Now consider the equation a(x2 + y2) + bx + cy + d = 0 (a, b, c ,d If a Substituting for x, y in terms of u, v we get d(u2 + v2) + bu – cv + a = 0 (†) Points (u, v) satisfying (†) correspond to points (x, y) satisfying (*). Hence we have the four cases: (a) a (b) a (c) a = 0, d (d) a = 0, d = 0. Straight line through O What is the image under w = f(z) = 1/z of line x = c? The line x = c maps to the set of points satisfying
This is the circle with centre (1/2c, 0), passing through the origin O. The half plane x > c maps to the interior of the disc. Let T be the transformation This is called a bilinear transformation as it can be rewritten as cwz + dw – az – b = 0 – an equation which is linear in each of its variables, z and w. Solving for w in terms of z, we see that the inverse of T is another bilinear transformation:
Notes z = –d/c 2. The set of bilinear transformations forms a group. In the formula for a bilinear transformation, if c
Setting z' = cz + d, z'' = 1/z', we obtain
If c = 0, we get an expression of type (*) immediately. It follows that any bilinear transformation can be obtained as the composition of linear transformations and the mapping f(z) = 1/z , all of which map lines and circles to lines and circles. Hence any bilinear transformation maps the set of lines and circles to itself. The following reult will be useful. Theorem 4.1 There exists a unique bilinear transformation which maps three given distinct points z1, z2, z3 onto three distinct points w1, w2, w3 respectively. Proof The algebraic expression for the bilinear transformation can be written as In practice, this means that in general if we allocate image points to three points in the z-plane, then the bilinear transformation will be completely determined. Conversely, if we want to find the image of a circle (say) under a given bilinear transformation, then it is sufficient to find the images of three points on the circle. Let a
That is, the x-axis maps to the unit circle having centre O. Also, z = a (a point in the upper half plane) maps to w = 0 (a point interior to the unit circle). Observing that the mapping is continuous, we deduce that the image of the upper half plane is the interior of the disc. As before, we set z = x + iy, w = The line y = c maps onto the ray
a is mapped to the region ea bounded by portions of circles and rays. This mapping is 1–1 if d – c < 2 As a particular case, the strip 0 < y < It is interesting to map the boundary points here. This mapping is useful in applications.
|
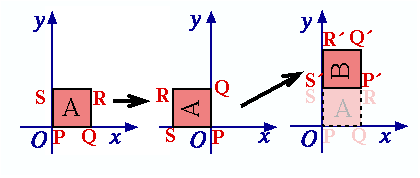 Example Consider the transformation w = iz + (i + 1).
Example Consider the transformation w = iz + (i + 1).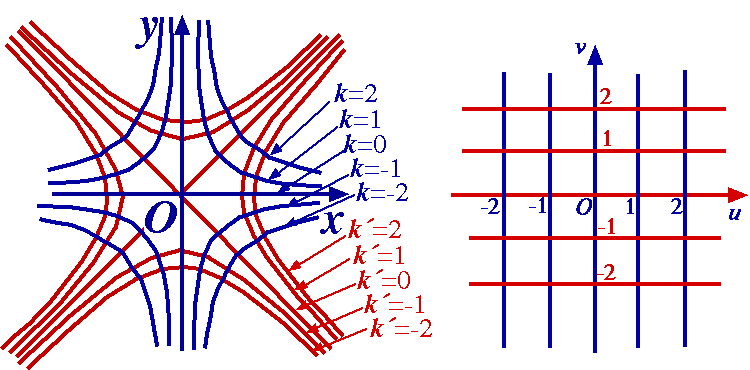

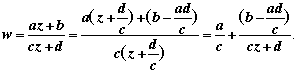
 We first consider the boundary. For z on x-axis, we have | z – a | = | z –
We first consider the boundary. For z on x-axis, we have | z – a | = | z – 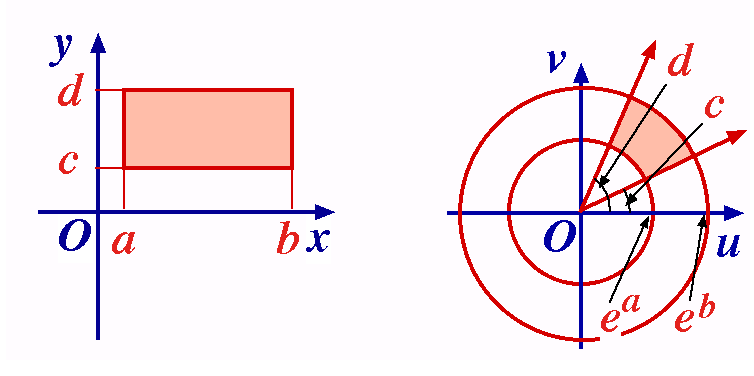 Combining these results, we see that the rectangular region
Combining these results, we see that the rectangular region 