ASTROID : Exploration

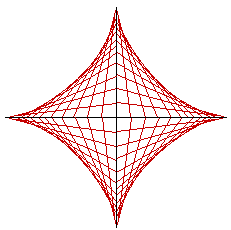
x^2/3 + y^2/3 = a^2/3.

The locus can also be defined parametrically as the set of points (x, y) for which

x = a cos³ t, y = a sin³ t (0 t < 2 ).

The area enclosed by the curve can be shown to be

            A = 3/8. a²,

and the length of the curve is

L = 6a.

We shall choose a = 1 here. What are the intercepts the curve makes on the axes?

Length of tangent

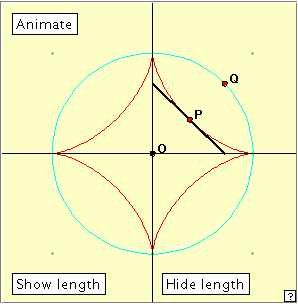
There are several interesting properties of the astroid which we can explore with our applets. The first concerns the length of a tangent to the curve, cut off by the axes. It is a variation of the program we used to generate the astroid.

Look at the applet linked at right. Move the point P around the astroid by manually moving the point Q on the circumcircle. At each point P we have drawn the tangent – in fact a segment of the tangent line cut off by the two axes. Can you make a conjecture about the length of this tangent segment?

Now click the ‘Show length’ button. What do you find?

Notice that in this construction we have chosen a = 1 (as indicated by the coordinate points in the figure), but we have left the length measurement in pixels: 100 pixels = 1 unit.

We conjecture the:

Theorem The tangent at any point P of an astroid is intercepted by the axes in a segment of constant length a.

This property may remind you of a series of so-called ‘ladder problems’. You might remember that the locus of the midpoint of a sliding ladder is a quadrant of a circle. Why is that different to the behaviour illustrated here? A reference to the ladder problems is given in the Bibliography below.

Locus of fixed point on tangent segment

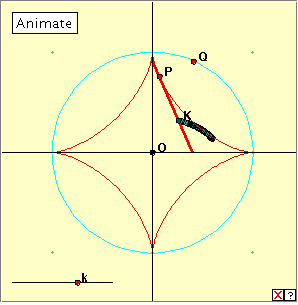
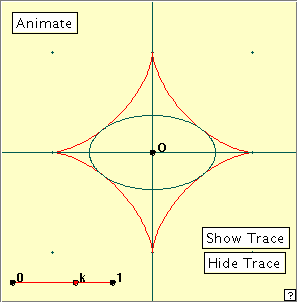
We observed above that the locus of the midpoint of a tangent segment is the quadrant of a circle. What happens for a more general fixed point?

Play with the applet linked at right. The point Q slides on the circumcircle as before to move P around the astroid. Alternatively, you can just click the ‘Animate’ button. The point k gives a value between 0 and 1 to determine (and fix) the position of K on the tangent segment. Choose some value of k and then make P traverse the astroid. What is the locus of K? Experiment with different values of k. What locus do you obtain when k is half way along the segment? Remember that you can delete a locus using the little red cross that appears at bottom right of the window.

We conjecture from this that as P travels around the astroid, any fixed point K on the tangent segment traces out an ellipse. If K is the midpoint of the segment, then this ellipse is a circle. This confirms the solution to the corresponding ladder problem.






The astroid as an envelope of ellipses

We can illustrate the above property a little differently using the applet at right.

Play with the linked applet. You can click the ‘Animate‘ button, or move the point k. What do you notice? Now click the ‘Show Trace‘ button and run the applet again.

The astroid is the envelope of ellipses having the same centre and orientation, and with the ‘sum of their axes’ being constant (= 2a).

Bibliography

A Book of Curves, Lockwood, E. H. (CUP 1967).

Wikipedia: http://en.wikipedia.org/wiki/Astroid

Wolfram MathWorld: http://mathworld.wolfram.com/Astroid.html

Ladder problems: http://www.mathematische-basteleien.de/ladder.htm