ellipse : exploration

Ellipse : Exploration

Properties

When the ellipse is studied analytically, it is the locus of points (x, y) in the plane which satisfy the equation

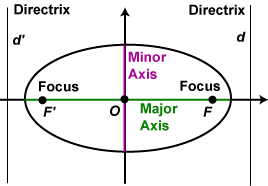
We associate with the ellipse two points F and F' (the foci) on the x-axis, and two lines d and d' (the directrices) perpendicular to the x-axis. The foci are equidistant from the origin, as are the directrices, and the actual distances are determined by the ellipse. The long axis of the ellipse is called the major axis; the short axis the minor axis. The origin O is the centre of the ellipse.

From the equation, we see that the ellipse cuts the x-axis in the points (a, 0), and the y-axis in (0, b). If we write e = b/a, the number e (< 1) is called the eccentricity of the ellipse. Notice e-llipse, e-less than 1 – a little help for remembering! When e = 1, we get the circle as a special case of the ellipse. Now the foci have coordinates (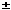 ae, 0), and the directrices meet the x-axis in the points ( 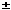a/e, 0). It is also known that b2 = a2(1 – e2).


Let us now investigate some interesting properties of the ellipse. Many of these properties are shared with the parabola and hyperbola, these curves all belonging to the family of conic sections.



Focus-directrix property

The adjacent diagram shows an applet of an ellipse with its foci and directrices. Click the diagram to open the applet, and then click the ‘Animate’ button and watch what happens. Now stop the animation (click the button again), and try various positions of P by manually dragging the point P along the x-axis.

We don’t expect the point Q on the ellipse to be equidistant from a focus and the corresponding directrix (or we would get the parabola). But some similar result might be true. Try measuring the distances for a number of positions of P. What can you say about the ratios of the distances? What is the eccentricity of this ellipse? State the property that you see illustrated here. Using the coordinates of the various points and lines given above, perhaps you can prove that the locus traced out here is an ellipse?

We have illustrated here a basic property of the ellipse: an ellipse is the locus of points Q which are in constant ratio e (< 1) from a fixed point (focus) and a fixed line (directrix).

Let Q(x, y) be the point tracing out the curve, and D the foot of the normal from Q to the directrix.
Then QF2 = e2PD2. In coordinates this becomes

                    (x – ae)2 + y2 = e2(a/e – x)2.

Expanding, and cancelling out the –2aex factors, we obtain

                 x2(1 – e2) + y2 = a2(1 – e2).

Substituting 1 – e2 = b2/a2 now gives

                x2/a2 + y2/b2 = 1

– the equation of the ellipse.





Focal chord property

Now look at this next applet. As usual, click the diagram to open the applet. QR is a chord through the focus F – a focal chord of the ellipse. We have drawn tangents at the ends of the focal chord.

What do you notice about the tangents? What appears to be true about segments TF and QR?

We see that the tangents at the end of a focal chord meet at a point T on the corresponding directrix. Further, the segment FT is perpendicular to the focal chord.

[Programming note It was surprisingly difficult to program this simple looking applet. JSP has no provision for finding the intersection of a line and a locus. So one can place point Q on the locus, and draw the line QF, but then how does one find the point R? We can probably do some hard calculations, but I was seeking a geometric solution. We can find T by taking the perpendicular to QR at F, but then how does one draw tangent TR? Let OF, QR meet the directrix in X, Z respectively, and let Q, R have projections Q', R' on the directrix. Using the focus-directrix property above, we can show that Q', R' divide X, Z internally and externally in the same ratio. Alternatively, (X, Z, Q' R') form a harmonic set. So constructing a suitable quadrangle based on XZQ'R' as base, we can locate R' and so R. See the source code for details.]

It is worth noting that this piece of interesting mathematics arises from overcoming a deficiency in the JSP programming!

A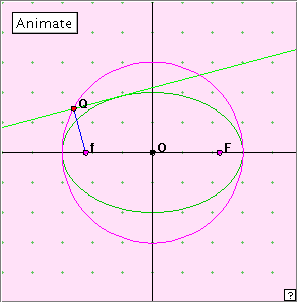n envelope property

In the diagram at right, the bounding circle of the ellipse is called its auxiliary circle. We can think of obtaining the ellipse from this by scaling down the y-values of the points on this circle. Now run the applet, using both the ‘Animate’ button and manually.

Describe what is happening here. How would you define the line which is generating the ellipse?

This is an easy way to generate the ellipse. Choosing any point Q on the auxiliary circle, and focus f, the line through Q perpendicular to Qf is tangent to the ellipse. Think about what happens when we choose the other focus F.








Focal distance sum property

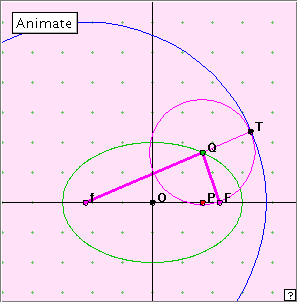
The ellipse is often defined in the following way. Given two points F’ and F, the locus of points P for which F’P + PF = constant is an ellipse. Can we illustrate this dynamically? Check out the adjacent applet, using the ‘Animate’ button, and moving point P manually along the x-axis.

We are looking at the sum of the lengths, fQ + FQ. What length is equal to FQ? What length is equal to the sum fQ + FQ? If this sum is constant, what would you expect the locus of T to be? Is it?!

Perhaps you can prove we obtain an ellipse here?
Hint: Use the values for fQ and QF defined by the focus-directrix property.

Since F and T both lie on the same (variable) circle centre Q, we have QF = QT, Hence fQ + QF = fQ + QT. If this is constant we expect the locus of the variable point T to be a circle centre f. This result is illustrated by the applet.

Could we change the roles of f and F here?

From the focus-directrix property of the ellipse, and using the standard coordinates, it is easy to see that if Q lies on this ellipse, QF = a + ex, and Qf = ex + a. That is, the sum of the distances from point Q to the foci is 2a.
Or, we can say, that this ellipse is the locus of all points Q for which Qf + QF = 2a.

So if Q is any point in the plane for which Qf + QF = 2a, it follows that Q must lie on this ellipse.








The parallel chords property

With the parabola we found that if we take a set of parallel chords (segments with endpoints on the parabola), then the midpoints all lie on a straight line parallel to the axis of the parabola. We find that parallel chords of the ellipse (and in fact the hyperbola) have a similar property. This occurs because these three curves belong to the same family – the conic sections.

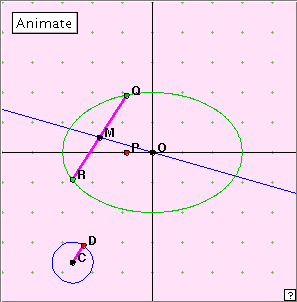
Open the applet. You can choose the direction of the chords using the little indicator dial at bottom left. Now click the ‘Animate’ button, or manually move the point P.

Notice the locus of the point M which is the midpoint of chord PQ. Describe this locus. What name would you suggest for it? For any fixed position of the chord, where do you think the tangents at Q, R might meet?

The locus of the midpoints of parallel chords of an ellipse is a straight line through the centre of the ellipse. This line is called a diameter of the ellipse. The tangents at the end of any such chord meet on the corresponding diameter.

[Programming note. I must confess to cheating with this program. The point Q (corresponding to P on the x-axis) is placed on the ellipse, but as noted above, there are problems with JSP in placing the other endpoint R on the ellipse. So the program locates the locus of the midpoints using O and the intersection T of the perpendicular to the relevant focal chord and the directrix. A parallel chord through Q meets this at M, and doubling the length of this segment gives R, which then lies on the ellipse.

This raises some interesting philosophical questions. Should the construction of an applet match the mathematical derivation of the result? Or will anything that works be acceptable? In fact, in this case, following our construction, we have shown that if M lies on the blue line, then R with QR = 2QM appears to lie on the ellipse!]


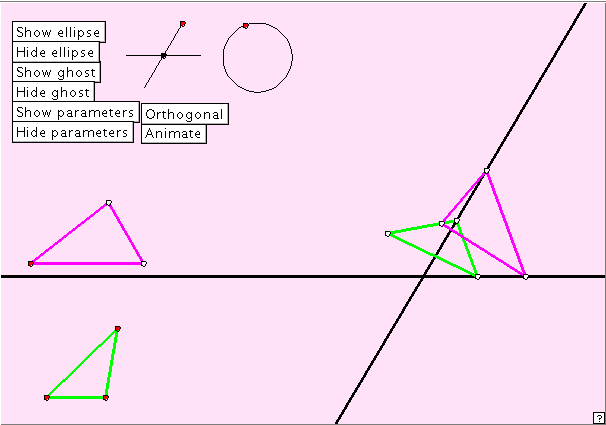
The three tangents property

The very pretty applet below illustrates an interesting occurrence of the ellipse. It comes from a web site by Paul Kunkel :

http://whistleralley.com/ellipse/ellipse.htm

On this site, the source code is freely available for download. It is always a pleasure to be able to make use of someone else’s hard work! The applet looks at the locus of the third vertex of a triangle for which the first two vertices slide along two inclined axes. Mathematics is full of surprises!


If you wish to learn more about the sliding triangle, check out the above web site.



Bibliography