|
CARDIOID : Inversion
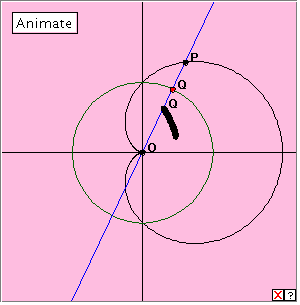
Click the linked diagram below and then the ‘Animate’ button to generate the inverse of the cardioid. Click the button again to stop the generation. Describe the mechanics of this generation. Clicking the little x at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle to get a better representation of the inverse curve. We have seen this curve before. What is it? The inverse curve here appears to be a parabola with its focus at the origin O. If you have already investigated the inverse of the parabola, then you will not be surprised at this result. For if the inversion transformation maps the parabola to the cardioid, we would expect the same mapping to map the cardioid to the parabola, since the inverse transformation interchanges pairs of points in the plane. We say that inversion has period 2. In fact, if we compare the polar equations of the cardioid and the parabola (with the focus as pole), we find that for the curves in this position, we have: Cardioid : r = 2a (1 + cos Parabola : l/r = 1 + cos |
 You might remember that we generated the heart shaped cardioid in graphical form using polar coordinates. The curve has one significant point called the cusp, which we took as the origin. If we are going to consider finding the inverse of this curve, the cusp i
You might remember that we generated the heart shaped cardioid in graphical form using polar coordinates. The curve has one significant point called the cusp, which we took as the origin. If we are going to consider finding the inverse of this curve, the cusp i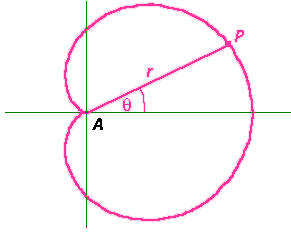 s the obvious point to take as the centre of our inversion. As usual, the radius of the circle is not important. For simplicity, in the applet it makes sense to use the circle locus of the driving point Q we used for generating the polar coordinates.
s the obvious point to take as the centre of our inversion. As usual, the radius of the circle is not important. For simplicity, in the applet it makes sense to use the circle locus of the driving point Q we used for generating the polar coordinates.