|
ELLIPSE : Inversion
where we have taken a = 3 and b = 2. In the second case we have used the polar form using one of the foci as the ‘pole’. This generates the ellipse nicely, but there are questions as to exactly where the origin then lies! Inversion about the centre O Let us then take a circle of inversion with centre at the origin. As usual, the radius chosen for the circle of inversion is not important here. In our applet the circle passes through the foci. There is no significance in this. Because the elliptic locus is constructed in two parts here – upper and lower – we have taken the inverse of the lower half and reflected it in the origin. The resulting inverse curve is not one we have encountered before. We get a more interesting result when we take the centre of inversion as one of the foci of the ellipse. The ellipse below was constructed using polar coordinates, taking F as the pole. This avoids the problem in the above applet of the ellipse appearing as the union of two halves. In the diagram below we have used the (magenta) circle of inversion as the construction circle of the ellipse. Click the linked diagram below, and then click the ‘Animate’ button to generate the inverse of the ellipse with respect to the focus F. Click the button again to stop the generation. Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle. Can you describe the construction? Do you recognize the inverse curve? The inverse curve here is a limaçon, a curve which we have seen before. It is easy to see why we might expect this. The polar equations are: Ellipse: l/r = 1 + e cos Limaçon: r = k + 2a cos
Bibliography Ellipse inversion video : http://video.aol.com/video-detail/ellipse-focus-inverse/2747576396
|
 We have seen how the ellipse occurs as a centrally symmetric curve with centre at the origin O, and two other special points F and F' known as the foci. So obviously if we are interested in finding curves inverse to the ellipse, we would consider circles of inversion at these special points. By symmetry it is clearly immaterial which focus we choose.
We have seen how the ellipse occurs as a centrally symmetric curve with centre at the origin O, and two other special points F and F' known as the foci. So obviously if we are interested in finding curves inverse to the ellipse, we would consider circles of inversion at these special points. By symmetry it is clearly immaterial which focus we choose.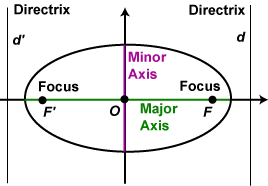 Each of the applets below constructs the ellipse with equation:
Each of the applets below constructs the ellipse with equation:
