 This inverse curve has a cusp at the origin, and in fact looks very much like the tractrix which we have seen before. In fact, it is a different curve with a different equation, known as the cissoid of Diocles. You may like to look it up on the web. The name cissoid means ivy-shaped, and Diocles, the Greek mathematician who discovered the curve, lived around the end of the second century BC.
This inverse curve has a cusp at the origin, and in fact looks very much like the tractrix which we have seen before. In fact, it is a different curve with a different equation, known as the cissoid of Diocles. You may like to look it up on the web. The name cissoid means ivy-shaped, and Diocles, the Greek mathematician who discovered the curve, lived around the end of the second century BC.
Inversion about the focus F
As mentioned above, the other obvious choice for the centre of inversion is the focus of the parabola. Let us now explore this case.

Click the adjacent diagram to activate the applet, and then click the ‘Animate’ button, or manually drag the red driver point along the x-axis. Again we have extended the range of this point well beyond the edges of the applet window in order to generate the inverse curve close to the origin. How would you describe the inverse curve? Do you recognize it?
The curve we obtain here is in fact the cardioid which we have discussed earlier. In this applet, the circle of inversion passes through the origin O, but the chosen radius is not important here. This applet is not difficult to construct, but I did have some problems getting the scales right.
You might like to compare the inversion process here with that of the catenary. Always look for patterns!
It is not surprising that we obtain the cardioid here. For the polar equation for the parabola, with the focus as the pole can be written as
If r1 represents the polar distance of the inverse points, and rr1 = 1, then r1 = (1 – cos 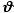 )/l which is essentially the polar equation of the cardioid.
)/l which is essentially the polar equation of the cardioid.
Bibliography
 If we wish to find the inverse of the parabola, there are two obvious choices of inversion centre: the origin O, or the focus F. In both these cases we derive a curve of interest, one of which we have already discussed here.
If we wish to find the inverse of the parabola, there are two obvious choices of inversion centre: the origin O, or the focus F. In both these cases we derive a curve of interest, one of which we have already discussed here.

