|
 The lemniscate has Cartesian equation The lemniscate has Cartesian equation
(x2 + y2)2 = a2(x2 – y2),
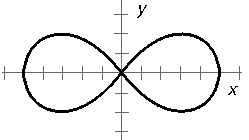 r2 = a2 cos 2 r2 = a2 cos 2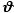 . .
We shall find that this curve is related to various other of our curves, but its main intrinsic property is that the curve encloses an area A = a2.
The lemniscate and its foci
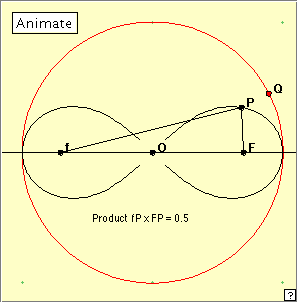 Let us take a = 1 in the equations for the lemniscate. The linked applet at right shows a lemniscate and two special points – the foci – which we shall label f and F. Points F and f are placed at a distance
Let us take a = 1 in the equations for the lemniscate. The linked applet at right shows a lemniscate and two special points – the foci – which we shall label f and F. Points F and f are placed at a distance 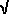 2 apart. 2 apart.
Play with the linked applet, using the ‘Animate’ button, but more particularly by manually dragging the point Q around the circumcircle. Notice the values of the product fP x FP. Within the numerical accuracy of the applet calculation, what appears to be true? Of what similar results does this remind you?
We note that this applet construction uses the polar equation of the lemniscate. For 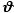 near near 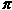 /4, the program omits the lemniscate points near the origin. More of these points would appear if the drawing had a larger scale. Notice too that for half the rotation of Q, no corresponding value of P appears. (Would we expect this?) /4, the program omits the lemniscate points near the origin. More of these points would appear if the drawing had a larger scale. Notice too that for half the rotation of Q, no corresponding value of P appears. (Would we expect this?)
We have the pretty conjecture that fP 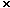 FP = constant = 1/2. (Notice the value we expect to obtain when P is at O.) This reminds us of corresponding results for the ellipse and hyperbola relating to the sum or difference of the distances to the foci. FP = constant = 1/2. (Notice the value we expect to obtain when P is at O.) This reminds us of corresponding results for the ellipse and hyperbola relating to the sum or difference of the distances to the foci.
In fact, if the foci lie at ( 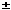 c, 0), and the distance product is c2, we get c, 0), and the distance product is c2, we get
fP2 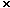 FP2 = [(x + c)2 + y2][ (x – c)2 + y2] = c4. FP2 = [(x + c)2 + y2][ (x – c)2 + y2] = c4.
Expanding and simplifying gives
(x2 + y2)2 = 2 c2(x2 – y2).
Setting c = 1/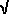 2, we obtain our equation for the lemniscate. 2, we obtain our equation for the lemniscate.
If we set fP = r', FP = r, the we have rr' = c2 = 1/2. This is called the bipolar equation of the lemniscate.
|
 The lemniscate has Cartesian equation
The lemniscate has Cartesian equation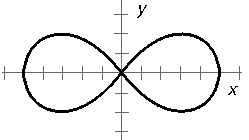 r2 = a2 cos 2
r2 = a2 cos 2