|
LIMAÇON : Exploration
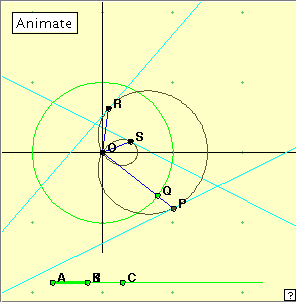
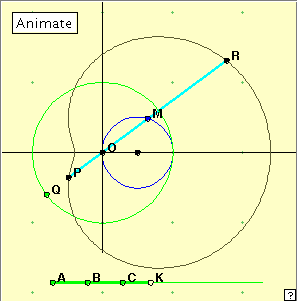
r = k + a cos This places the curve in the position shown at right. We can simplify this equation by scaling the coordinates suitably, to get r = k + cos and we shall use this form here. When k = 1, the equation is that of a cardioid; that is, a cardioid is a special type of limaçon. When k = 1/2, the limaçon is called a trisectrix, a curve of special historical interest. (This curve is not to be confused with the tractrix which we shall discuss elsewhere.) It is not helpful to try to find the Cartesian equation of the general limaçon, but we can find the Cartesian coordinates of a point P(x, y) of the curve using the formulae x = r cos The members of the limaçon family have one particular point of interest on the curve. In the case of the cardioid we call it the cusp – it is a point where no tangent can be defined, as the curve has no slope there. For limaçons close to the cardioid, there is still a noticeable point, but it is not a cusp; it is generally called a node. This term can also be used where the curve crosses itself, although the term cross-over point is very descriptive. Click on the figure at right to open the applet. You can operate the applet by clicking the ‘Animate‘ button, or by manually dragging the point Q around the green circle. The position of point K on the bottom segment governs the shape of the lemniscate being generated: distance AK = k in the equation of the limaçon. Consider the limaçon shapes for different positions of the sliding point K. Notice that AB = BC = 1/2. For what position of K do we get the cardioid? Note the shape of the trisectrix when K coincides with point B. Do you think the circle belongs to this family of limaçons? In how many ways? Notice the values of k given above in the introduction for the cardioid and trisectrix. We observe that as K moves to the right, the limaçon flattens and then bulges to the left on the left hand side of the curve. This suggests that we should obtain the circle as the limiting case of the limaçon as k gets very large. This makes sense, because as k increases in size the term cos Experiment with the applet linked at right. We know that when the slider point K is at C we obtain the cardioid and the tangents are parallel. Does this happen for any other position of K? Or perhaps the tangents behave in some other interesting way? Or perhaps there is some other interesting behaviour which does not involve the tangents at all? [Hint: think about the positions of the three points P, R, S for various positions of K .] There seems to be no interesting new tangent behaviour, apart from the fact that near the ends of the k-scale the tangents approach an equilateral triangle formation. We expect this as the limaçon approaches a circular shape. But, did you notice anything about the positions of the tangent points?
Conjecture If O is the crosss-over point of a trisectrix, and P, R, S are three points on the curve such that the lines OP, OR, OS make angles of 120° at O, then the points P, R, S are collinear. http://homepage.mac.com/paulscott.info/trisectrix/
The little exercise above gives us some insight into how mathematical research is done. Often a new result is obtained by varying the conditions of an existing problem. Here I was looking for some alternative behaviour of the three tangents, and just happened to notice this (supposedly) new result. From the applet the result appears to be true for all positions of the generating point Q. This means that the result is very likely to be true. However, this does not constitute a proof. It required some complicated mathematical calculation to verify this result.
Play with the applet linked at right. Investigate the length of the chord through the cusp / cross-over point, and also the locus of the midpoint M. What conjectures can you make? Can you prove your conjectures? The general equation of the limaçon is r = k + cos Length = (k + cos Again, for the cardioid, the locus of the midpoint is the circle centre (1/2, 0) and radius 1/2. I was really quite surprised to find that this appears to remain true for all limaçons in the family. Let’s see if we can prove it. In fact, the proof is quite easy. In the diagram, let the blue circle meet the positive x-axis in point C. Now since M is the midpoint of the chord, MP = k, and so from the equation of the limaçon, OM = cos So we have proved the Theorem For a general limaçon with equation r = k + cos
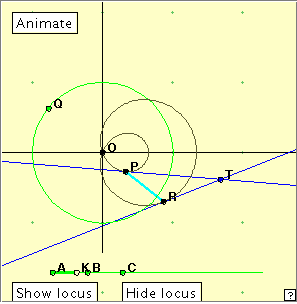
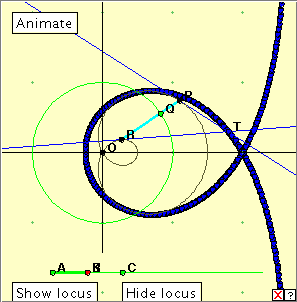
Check out the applet at right. You can show or hide the locus of T using the buttons. If you want to clear a drawn locus, clickthe little red cross which will appear at bottom right of the window. Investigate the behaviour of T for various positions of K. We notice that if the curve is not a cardioid, there is a position of Q for which T ’goes to infinity’. Why is this so?
It is interesting to investigate the different loci of T for varying positions of K. For K lying between A and C (0 < k < 2a) we appear to obtain a curve known as a right strophoid (left). Bibliography A Book of Curves, Lockwood, E. H. (Cambridge University Press (1967). New trisectrix result: http://homepage.mac.com/paulscott.info/trisectrix/ Wikipedia : http://en.wikipedia.org/wiki/Limaçon Wolfram MathWorld: http://mathworld.wolfram.com/Limacon.html |
 Properties
Properties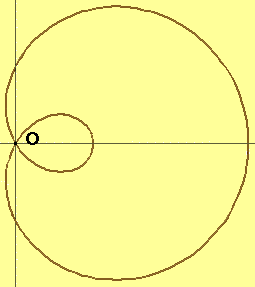 As we have already observed, there is a whole family of curves called limaçons. A limaçon is best describe by a polar equation of the form:
As we have already observed, there is a whole family of curves called limaçons. A limaçon is best describe by a polar equation of the form: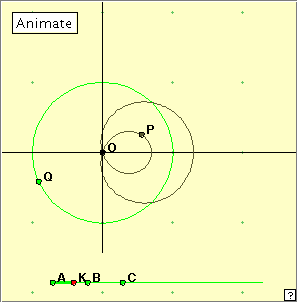
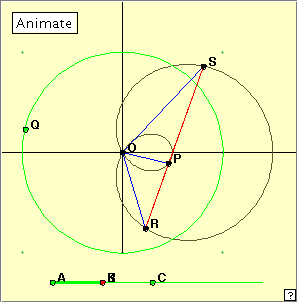
 When the curve is a cardioid, the tangent at the cusp is horizontal and meets the other vertical tangent at (2, 0). In all other cases the tangents at these two points are both vertical and meet ’at infinity’.
When the curve is a cardioid, the tangent at the cusp is horizontal and meets the other vertical tangent at (2, 0). In all other cases the tangents at these two points are both vertical and meet ’at infinity’.