|
LIMAÇON : Generation
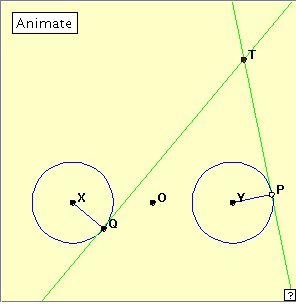
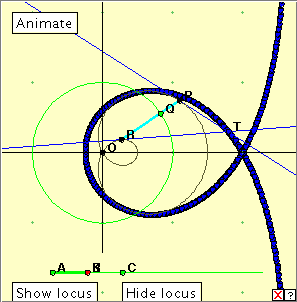
The applet linked below generates the limaçon. The generation uses a fixed base circle, and a fixed point A outside it. Click the diagram to open the applet, and then click the ‘Animate’ button to generate the limaçon. Click the button again to stop the generation. Clicking the little red x at bottom right will clear the drawing from the applet window. Now drag the red point slowly around the circle. Can you describe the construction?
The method of construction is to construct circles centred at the red point and passing through the fixed point A. The limaçon occurs as the envelope of these circles. Reflection This method of generating the limaçon creates an envelope of circles, thus determining the shape. It is clear from its appearance that the limaçon is a close relative of the cardioid. This is also clear from the method of construction. With the cardioid we choose a base circle and a fixed point A on the circle. With the limaçon we choose a base circle and a fixed point A outside the circle. The obvious question to ask is, what happens if we carry out the construction using a base circle and a fixed point inside the circle.
In fact, the term limaçon is used for a whole family of curves of which the above curve and the cardioid are members. By taking the point A at the centre of the base circle, we expect the circle to be a member of this family too. Here is another pretty way of generating a limaçon. In this case we have two given fixed circles in the plane. An angle PTQ of fixed size moves so that side PT is tangent to Circle 1 at P, and side TQ is tangent to Circle 2 at Q. Now vertex T generates a limaçon. In fact, four limaçons can be generated using this method. Can you see why?
This method of generation is sometimes given in terms of a triangle with two of its sides forming tangents to the given circle, but the third side of the triangle plays no part in the construction.
Occurrences We are pretty hard pressed to find any real life occurrences of the limaçon. The trisectrix occurs as part of the logo of a music company, and the limaçon snail bears little actual resemblance to the curve!
|
The name ‘limaçon’ is derived from the Latin word limax for ‘snail’. (It is pronounced with a soft ‘c ’.) It was used of this shape by the French scientist Gilles Roberval around 1635. The curve was actually known much earlier in 1525, when it appeared in a publication by Albrecht Dürer, although without the name.
