|
 Because of the close relationship between the hyperbola and the ellipse, we might expect the pedal curves of the hyperbola to be similar to the those of the ellipse. This turns out to be true and false! As usual, we take normals from point K to the tangents to the hyperbola. The locus of these intersection points is the pedal curve with respect to K. Because of the close relationship between the hyperbola and the ellipse, we might expect the pedal curves of the hyperbola to be similar to the those of the ellipse. This turns out to be true and false! As usual, we take normals from point K to the tangents to the hyperbola. The locus of these intersection points is the pedal curve with respect to K.
Click the linked diagram below, and then click the ‘Animate’ button to generate the pedal curve of the hyperbola with respect to the point K. Clicking the little red x which appears at bottom right will clear the drawing from the applet window. Now drag the red point Q slowly along the x-axis. Can you describe the construction? Experiment with different positions of the point K. Of special interest is when K lies at the centre of the hyperbola, and when K lies at a focus of the hyperbola.
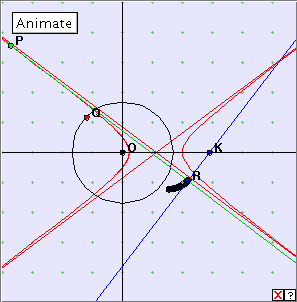
When K lies at the centre of the hyperbola, the pedal curve turns out to be a lemniscate. When K lies at a focus we again obtain the circle, as for the ellipse.
|