13. PORISMS
Introduction Porism: A proposition that uncovers the possibility of finding such conditions as to make a specific problem capable of innumerable solutions. Porism: A situation where there are either no possible solutions or an infinite number. This probably makes about as much sense as the first! The idea is best seen by means of example. We shall give several examples. The first of these porisms is due to the geometer Jakob Steiner – we have come across him before. It makes an ideal link with the last chapter, as it is easily proved using inversion.
|
|
Steiner’s Porism
Case 1: No closed chain exists Case 2: Closed chain exists (I) Case 3: Closed chain exists (II) Proof of Steiner’s Porism Circles S and T determine a coaxial system with a limit point X say. Inverting the figure using an inversion with centre X, S and T map to concentric circles |
| If S and T belong to a system of coaxial circles with limiting points X and Y, then there is an orthogonal system of circles passing through X and Y. Under inversion in a circle with centre X, the orthogonal system maps to a pencil of straight lines through X', the inverse of X. Now S, T, and other circles of the original coaxial system map to a system of circles orthogonal to the lines of this pencil: that is, the system of concentric circles with centre X'. |
Let S and T be two fixed circles, one contained within the other. We draw a polygonal sequence of lines with vertices on the larger circle and lines tangent to the inner circle. The sequence may close as shown to form a polygon (triangle here), or not close. Poncelet’s Porism states:
The illustration for closing shows a triangle, but the porism remains true for any n-sided polygon. We notice that the previous pretty proof no longer works here. We can certainly invert circles S and T into concentric circles with common centre X, but the edges of the polygonal path map to circles through X which is not helpful. The actual proof of the Poncelet Porism is beyond us here.
|
P
It seems likely that this result can be extended to general n-gons. http://mathforum.org/kb/message.jspa?messageID=1093830&tstart=0 |
 Jakob Steiner
Jakob Steiner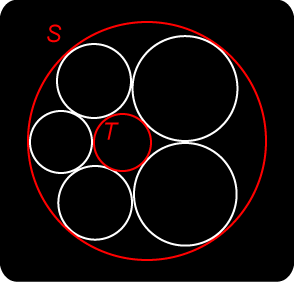 We are given two fixed circles S and T, one contained within the other.
We are given two fixed circles S and T, one contained within the other.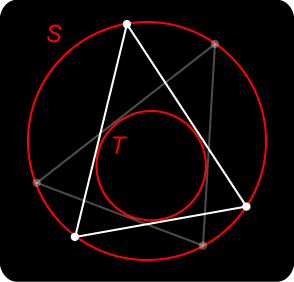 Poncelet’s Porism
Poncelet’s Porism Jean-Victor Poncelet
Jean-Victor Poncelet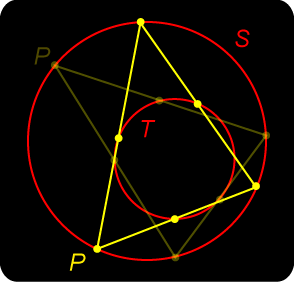 Midpoint Porism
Midpoint Porism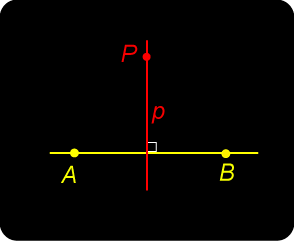 Analysis
Analysis