7. APOLLONIUS CIRCLE
|
|
To fully understand the Apollonius circle, we return briefly to cross ratios.
Proof Starting with (*): |
|
|
Harmonic Pencil We have defined a collinear set of points A, B; C, D to be harmonic if
|
| A lemma is a ‘helping theorem’. In German the word is Hilf-satz. |
A
Proof We are given that the pencil P(A, B, X, Y) is harmonic. Also, P lies on the circle on XY as diameter, so PX |
|
Extensions 1. If A, B are two points on a line, then the midpoint of segment AB is the harmonic conjugate of ‘the point at infinity’ of the line AB. |
 Apollonius of Perga (ca. 262 BC – ca. 190 BC) was a Greek geometer and astronomer, of the Alexandrian school, noted for his writings on conic sections. It was Apollonius who gave the ellipse, the parabola, and the hyperbola the names by which we know them. The Apollonius crater on the moon was named in his honor.
Apollonius of Perga (ca. 262 BC – ca. 190 BC) was a Greek geometer and astronomer, of the Alexandrian school, noted for his writings on conic sections. It was Apollonius who gave the ellipse, the parabola, and the hyperbola the names by which we know them. The Apollonius crater on the moon was named in his honor.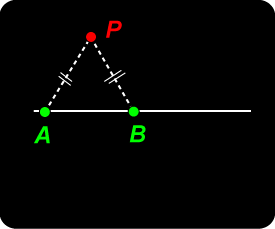 Let A , B be two fixed points on a line. Our problem is to find the locus of a point P which moves so that the ratio of its distances from A and B is constant.
Let A , B be two fixed points on a line. Our problem is to find the locus of a point P which moves so that the ratio of its distances from A and B is constant.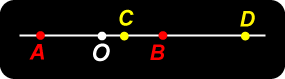 Harmonic Set
Harmonic Set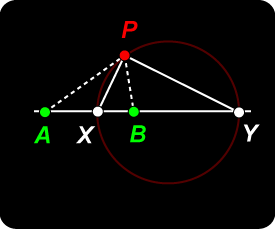 The Circle
The Circle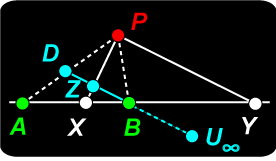 Referring to the adjacent diagram, we draw line DZB parallel to YP. We are going to follow a useful convention and define a ‘point at infinity’,
Referring to the adjacent diagram, we draw line DZB parallel to YP. We are going to follow a useful convention and define a ‘point at infinity’, 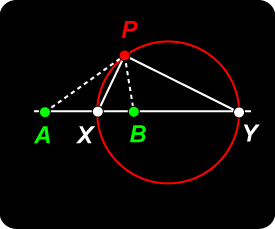 Converse Result
Converse Result It follows that for all positions of P
It follows that for all positions of P