 The game The game
This old Spirograph™ game shows the basis of the construction. There is a large fixed circle of gear teeth (in fact the picture shows a ring with two geared edges, but this is necessary for the physical construction). A smaller disk with gear teeth is made to rotate inside or outside this large circle, with the gear teeth in contact. The smaller disk has a variety of holes in it, placed at different distances from the boundary. A pen placed in one of these holes then describes a spirograph pattern. The use of different sized disks and different holes gives a wide variety of interesting patterns. It is these we wish to analyze here.
|
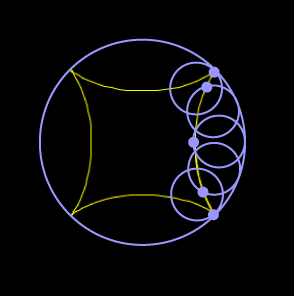
Here is an example. The small blue circle rolls around the inside of the large fixed blue circle in an anti-clockwise direction (say). We have chosen a point on the boundary of the small circle. As the small circle rolls, this point traces out the yellow arc. If we continue rolling the small circle, the point traces out the whole of the yellow figure. |
The Java applet
Now open the Java applet. It is written by Anu Garg, a graduate in computer science, who in 1994 founded Wordsmith.org . Anu Garg has kindly made this beautiful applet available for free download. Place the applet window so that (if possible!) you can see the applet and at least the bottom part of this page.
We first check out the controls at the right. Play with these controls as we discuss them.
The top slider gives the radius of the fixed circle between 0 and 100.
The second slider gives the radius of the small rolling circle.
• The radius values here vary between –50 and +50. Since the radius is always positive, how are we to interpret this?
The third slider gives the moving circle offset. This gives the distance of the tracing point from the centre of the moving circle. Notice that it can extend beyond the radius of the circle!
The Red / Green / Blue sliders allow you to change the colour of the traced path in standard RGB form. Play with these if you have not worked with RGB colours before.
The Revolutions slider is very useful Having chosen numbers for the top three sliders, moving this slider from left to right allows you to see how the construction takes place.
The remaining controls are self-evident. My preference is to use the line construction on the dark canvas with the Chirp off, or at least turned down very low.
# If the radius is negative, the rolling circle is inside the fixed circle; if positive, outside.
Special curves
Historically there has been some interest in studying various curves and classifying them. A standard reference is A book of curves by E. H. Lockwood (Cambridge University Press). Just for the record:
There are four different names for types of spirograph curve, depending on the positions of the rolling circle and the tracing point. These are:
| |
rolling circle is ...
|
|
tracing point is ...
|
inside the fixed circle
|
outside the fixed circle
|
|
on the circle
|
hypocycloid
|
epicycloid
|
|
on or inside the circle
|
hypotrochoid
|
epitrochoid
|
I can’t imagine that you would ever need to know these, except perhaps for an advanced session of Trivial Pursuit!
A number of classical curves occur in this way, and are easy to generate using the applet. We shall use the short-hand notation {R, r, o} to give the values for the first three sliders. Here are some exercises for you. The graphics are not ‘pretty’ but they do have distinctive shapes.
•
|
Applet settings
|
Name of curve
|
Questions and comments
|
|
{50, 50, 50}
|
Cardioid
|
Why the name? |
|
{50, 50, 100}
|
Limaçon
|
Is the limaçon related to the cardioid? |
|
{100, -25, 25}
|
Astroid
|
Normally pictured rotated 45°. |
|
{60, 30, 30}
|
Nephroid
|
Why the name? |
|
{99, -33, 33}
|
Deltoid
|
Do the symmetries of the figures relate to the applet numbers? |
|
{100, -25, 75}
|
Quadrifolium
|
We probably started off using the spirograph applet in a fairly arbitrary way, but already you may be becoming aware of some structure in relation to the applet settings. We shall go on to investigate this, but first let’s check the special curves obtained above.
#
 |
 |
 |
 |
 |
 |
|
Cardioid
|
Limaçon
|
Astroid
|
Nephroid
|
Deltoid
|
Quadrifolium
|
Cardioid means heart-shaped (from Greek, kardia = heart); limaçon (French, literally snail) – special case is the cardioid; astroid means star-shaped (from Greek); nephroid means kidney-shaped (from Greek); deltoid means triangular (compare Greek capital letter delta); quadrifolium means four leaves (from Latin).
Symmetry
If we look at the above pictures of the astroid, nephroid, deltoid and quadrifolium, we notice that they each have some rotational symmetry. For example, you can rotate the astroid about its centre through 90° and it will map to itself (remain unchanged). In fact, it has four-fold rotational symmetry about its centre: you can rotate it through 0°, 90°, 180°, and 270° (and any further multiples of 90°). If you labelled one of the vertices P say, there are four distinct positions this label might take under rotation.
In general we say that a figure has n-fold rotational symmetry about its centre if the figure maps to itself under rotations about its centre of 0, 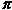 /n, 2 /n, 2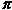 /n, ... , (n – 1) /n, ... , (n – 1)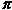 /n, where we have switched to radian notation. Radian notation is in fact usually simpler to use. Just remember, /n, where we have switched to radian notation. Radian notation is in fact usually simpler to use. Just remember, 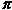 = 180°. = 180°.
• Sketch figures which has 2-fold symmetry, 3-fold symmetry, 4-fold symmetry, 5-fold symmetry.
List the angles of rotation for each, in degree measure and in radian measure.
What would a figure with 1-fold symmetry look like?
• Look at the capital letters of the alphabet in a simple font. What symmetries can you find here?
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

# Examples we have seen for 2-, 3- and 4-fold symmetry are respectively the nephroid, deltoid, astroid and quadrifolium. A regular pentagon has 5-fold symmetry. A caardioid is a figure with 1-fold rotational symmetry: the only rotation within a complete turn which maps it to itself is a rotation through 0° (0 radians).
# The letters of the alphabet have many symmetries, but they are mostly reflective. Notice here that H, I, N, S and Z have 2-fold symmetry, X has 2-fold symmetry, or 4-fold if it is drawn sufficiently squat, and we might say that O has 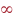 -fold symmetry if it is an exact circle. The other letters have 1-fold symmetry. -fold symmetry if it is an exact circle. The other letters have 1-fold symmetry.
Number properties
If in the applet we look at {60, r, *} where * can be anything (not too small!), and r runs through its range of values, we find that some of the patterns obtained are very simple, while others are quite complicated. Let’s try to figure out why this is so.
• Look at the six simple shapes illustrated above, and then look at the values of R and r used to generate them. What do you notice? Is there any relationship between the numbers which helps explain the nature of the symmetry of the resulting figure?
• In the applet, look at {60,  30, *}, {60, 30, *}, {60,  20, *}, {60, 20, *}, {60,  15, *}, {60, 15, *}, {60,  12, *}, {60, 12, *}, {60,  10, *}, {60, 10, *}, {60,  5, *}. What do you notice? Check out some examples of your own. 5, *}. What do you notice? Check out some examples of your own.
• Think about the rotating wheels with their engaging gear teeth. Do your observations fit with what one might expect from mechanical considerations?

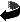
In general, assume r, R are positive integers. We say that r is a divisor of R, if r divides R exactly. That is, there exists some positive integer k with R = rk. For example, 5, 10, 12, 15, 20 and 30 are divisors of 60.
# In our Spirograph applet we have seen that values of R, r (or –r) where r is a divisor of R give rise to relatively simple patterns – in fact, patterns with k-symmetry. In terms of the rotating wheels we would expect this. For if r is a divisor of R, then the rotating wheel rotates exactly k times before it gets back to its starting position. This means that the trace path has exactly k identical components, leading to k-symmetry in the figure.
• Now in the applet, look at {60,  50, *}, {60, 50, *}, {60,  45, *}, {60, 45, *}, {60,  40, *}, {60, 40, *}, {60,  36, *}, {60, 36, *}, {60,  35, *}, {60, 35, *}, {60,  32, *}. Can you explain what is happening here? Check out some examples of your own. 32, *}. Can you explain what is happening here? Check out some examples of your own.
• Here is a different lot of settings. Look at {75, 50, *}, {66, 44, *}, {60, 40, *}, {54, 36, *}, {48, 32, *}. What do you notice here?
• With this new observation, perhaps you can now explain what is happening, and relate it to the rotating wheels?

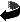
# We observe that it is the ratio of R and r which is important in determining the Spirograph figure and the corresponding symmetry. Figures with the same ratio r/R are the same (apart from some small variation due to the pixelated nature of the screen). In fact, our experiments indicate that if the ratio r/R reduces to r'/R', and this fraction is in ‘lowest terms’, then the Spirograph figure has R'-symmetry. So for example, {60, 40, *} gives r/R' = 40/60 = 2/3, resulting in 3-symmetry. Mechanically, if the small wheel has 2/3 the number of gear teeth of the fixed wheel, if the small wheel rotates three times, it will make two circuits of the fixed wheel before finishing up in its starting position. This gives 3-symmetry of the figure.
We observe that in the case where r is a divisor of R, r/R = 1/k, which is obviously in ‘lowest terms’, so the k-symmetry obtained there corresponds to this more general rule.
Some pattern sequences
We finish this chapter by looking at some families of Spirograph figures. We begin with:
 Flower patterns Flower patterns
• In the applet, check out {99, –33, 66}. You should obtain the illustrated trifoil consisting of three symmetrically placed ‘petals’ or ‘leaves’.
• Try to generate ‘flowers’ with four, five, six, ... petals. Can you explain your choice of R and r? What about the choice of o?

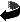
# In the case of the trifoil, the ratio R/r = 1/3 is obviously a good choice in order to obtain the symmetry. To explain the value of o, think of the circle of radius 33 rotating inside the fixed circle of radius 99. We want our ‘petals’ to originate at the origin. What value offset would be required for this? We need 66 which when added to 33 sums to the large radius 99.
# Possible choices for flowers having more ‘petals’ are {100, –25, 75}, {100, –20, 80}, ... .
Curved polygons
Here is another set of patterns. Try to continue the sequence for a few steps. If you feel inspired, you might also try to relate the figure to the choice of numbers.
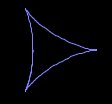
We might think of the deltoid and the astroid as the first members of a family of curvilinear polygons – regular polygons, but with sides that arc inwards.
We already know (above) that {99, –33, 33} generates a deltoid, and {100, –25, 25} an astroid.
• Find the settings for the next polygons in this sequence.
Straight line figures
There are a great number of fascinating figures which can be obtained by selecting small values of r, along with a reasonably large offset o. You might like to investigate these.
http://en.wikipedia.org/wiki/Spirograph
The mathematics of the spirograph: http://www.iw.net/~nnburk/Presentation1.pdf
A Book of Curves, Lockwood, E. H. (Cambridge University Press 1967)
|
 The game
The game






