|
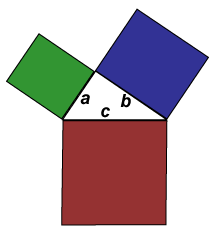
The standard diagram of Pythagoras’s theorem shows a right-angled triangle with squares attached to each edge. If the side lengths of the right-angles triangle are a, b and c as shown, then according to Pythagoras, a2 + b2 = c2. It is less well known that the theorem can be illustrated with other similar shapes attached to the sides, for example, triangles. This is because the areas of similar figures are proportional to the squares of the side-lengths. In 1922, this suggested to US professor Harry Bradley the following problem. Problem T4. Give a 5-piece triangle dissection to illustrate a2 + b2 = c2. This will have the effect of dissecting a large triangle of side length c into two smaller triangles of side lengths a and b. We demonstrate Bradley’s dissection. Suppose that a
|
|||||||||||
 5. TRIANGLES – PYTHAGORAS
5. TRIANGLES – PYTHAGORAS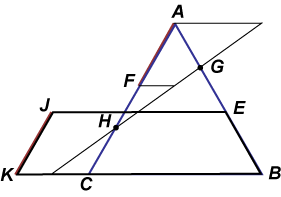
 Let’s take the c-triangle (at right) and
Let’s take the c-triangle (at right) and