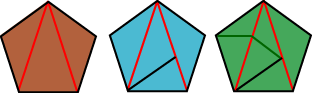
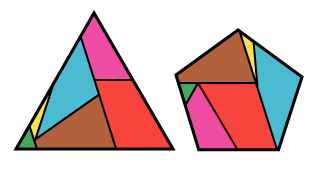 Since pentagons do not tessellate the plane, or form easily into strips, we might epect dissections of pentagons to present rather more of a challenge than the dissections we have seen thus far. At right we show 6-piece dissections of a triangle to a pentagon and a square to a pentagon. These can be obtained by strip dissections, but not of any obvious or intuitive kind. For details see here. However, the pentagon does have an interesting property with pretty consequences. Let Since pentagons do not tessellate the plane, or form easily into strips, we might epect dissections of pentagons to present rather more of a challenge than the dissections we have seen thus far. At right we show 6-piece dissections of a triangle to a pentagon and a square to a pentagon. These can be obtained by strip dissections, but not of any obvious or intuitive kind. For details see here. However, the pentagon does have an interesting property with pretty consequences. Let 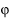 = = 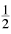 (1 + (1 + 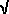 5) denote the golden ratio (strictly 5) denote the golden ratio (strictly 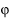 /1). Then you can check that /1). Then you can check that 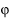 – 1 = 1/ – 1 = 1/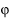 . Now a regular pentagon of side length 1 has diagonals of length . Now a regular pentagon of side length 1 has diagonals of length 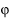 . .
 If a polygon is to be dissected in a ‘pretty’ way, we might hope to use its natural subdivisions. For the pentagon, these might include the subdivisions If a polygon is to be dissected in a ‘pretty’ way, we might hope to use its natural subdivisions. For the pentagon, these might include the subdivisions 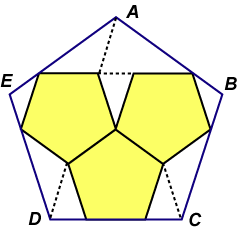 at left. Black segments have length 1 (say), red segments have length at left. Black segments have length 1 (say), red segments have length 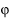 , green segments have length , green segments have length 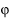 – 1. – 1.
In 1956 Dudley Langford solved the following pretty problem:
Problem P1. Find a 12-piece dissection of 5 pentagons to 1 pentagon.
We might ask, ‘Why five?’ Well, if the small pentagons have side-length 1, the large single pentagon must have side length 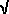 5 (an argument using areas) which is encouraging! Langford probably realized he was on to a good thing when he saw that 3 1-pentagons sit nicely inside a 5 (an argument using areas) which is encouraging! Langford probably realized he was on to a good thing when he saw that 3 1-pentagons sit nicely inside a 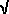 5 - pentagon. Check lengths CD, DE, DA for example to see if you get 5 - pentagon. Check lengths CD, DE, DA for example to see if you get 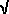 5. (For example, CD = ( 5. (For example, CD = (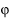 – 1) + 1 + ( – 1) + 1 + (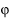 – 1) = 2 – 1) = 2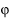 – 1 = – 1 = 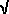 5.) Now do the remaining pieces make up two small pentagons? What do you think? Check here. Finally, there is a very nice 15-piece dissection based on the blue pentagon above. 5.) Now do the remaining pieces make up two small pentagons? What do you think? Check here. Finally, there is a very nice 15-piece dissection based on the blue pentagon above.
|
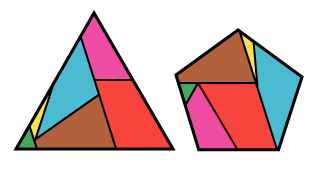 Since pentagons do not tessellate the plane, or form easily into strips, we might epect dissections of pentagons to present rather more of a challenge than the dissections we have seen thus far. At right we show 6-piece dissections of a triangle to a pentagon and a square to a pentagon. These can be obtained by strip dissections, but not of any obvious or intuitive kind. For details see here. However, the pentagon does have an interesting property with pretty consequences. Let
Since pentagons do not tessellate the plane, or form easily into strips, we might epect dissections of pentagons to present rather more of a challenge than the dissections we have seen thus far. At right we show 6-piece dissections of a triangle to a pentagon and a square to a pentagon. These can be obtained by strip dissections, but not of any obvious or intuitive kind. For details see here. However, the pentagon does have an interesting property with pretty consequences. Let  If a polygon is to be dissected in a ‘pretty’ way, we might hope to use its natural subdivisions. For the pentagon, these might include the subdivisions
If a polygon is to be dissected in a ‘pretty’ way, we might hope to use its natural subdivisions. For the pentagon, these might include the subdivisions  at left. Black segments have length 1 (say), red segments have length
at left. Black segments have length 1 (say), red segments have length