|
|
 |
|
 |
Legend
The Dragon Curve takes its name from an ancient Chinese creation myth: ‘At the beginning of time when primal chaos reigned over the world and all was enclosed in darkness a great earthquake shook the plain of Hao Sung. The earthquake caused the plain to fold over on itself once and then again and again, many times until the plain had assumed the form of a dragon. Breathing in the mists of time the dragon came to life exhaling immense jets of flame. Flapping its great wings it flew into the endless void surrounding the world, breathing fire to heat and light the world.’ There is an interesting story behind this legend. Years ago, my Honours student, Matthew Brown, included it in a project, and it seemed good to include in the book. When Bill Beaumont expressed doubt about the Chinese knowledge of the dragon curve, I approached Matthew, who then confessed he had made the whole thing up! PRS |
 |
| Some paper folding (I)
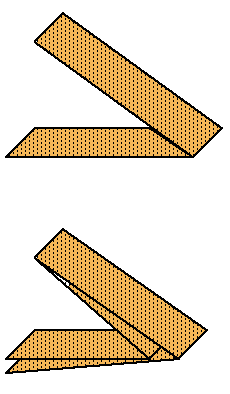
To construct the dragon curve, we need to understand the way the plain in the myth actually folds. 1. (a) Lay a long thin strip of paper flat on the table, and fold it over, right over left. Unfolding it will now give a V shape. (b) Fold the strip back again as it was, and fold the folded strip again, right over left. Unfolding the paper, you should now get angles V V L in this order. |
(c) Continue this process several more times, and record your results.
It will be easier if we replace V by 1 and L by 0. You should now have a sequence like this: 1 We notice immediately that each of these rows of 1s and 0s starts off like the one preceding it. Now we try to discover more about these rows. |
| Some paper folding (II)
2. (a) What is the middle digit in each row? Can you explain why these are all the same? (b) Can you see that each row has a sort of reflective symmetry about this digit? Thinking of the paper folding, can you explain why this occurs? (c) How many digits are there in each row? Why do these numbers make us think of powers of 2? It is clear that powers of 2 have an important part to play here. You should now be able to construct the paper-folding sequence. If we number the position of the digits from the left by 1, 2, 3, ... we get:
However, this is still rather clumsy, as we have to work out each value in turn. |
Now let f(n) the value 0 or 1 corresponding to the nth fold. Then from our argument about the centre folds,
f(n) = 1 for n = 1, 2, 4, 8, ... However from our investigation we might also guess or conjecture that: You might have other conjectures too. Such conjectures are a very important part of mathematics. But conjectures may be wrong! Can we prove these results? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The matter of proof
We give a brief outline of the reasons why our conjectures are true. Consider the values we obtained before in the rows of the table:
Because of the reflective property of our paper folding (reflecting in 2, 4, 8, ... ), the values of f(n) in the lower line have the repeating pattern 1 1 0 • 1 0 0 • 1 1 0 • 1 0 0 • . . . . |
It follows that
Also, if we consider the reflective property as it applies to the even values of n, we obtain
Since the method of formation and the initial values are the same, the two rows of 0s and 1s are also the same. This shows that f(n) = f(2n) for n = 1, 2, 3, ... as required. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| The dragon curve
The dragon curve is simply the shape formed by our repeatedly folded strip of paper, but with all folds making angles of 90°. The curve is generated by two procedures (see box below), each of which calls upon the other. This is a short program, but it is complex in its structure. To see just what is happening, work through it for levels 0, 1, 2 and 3.
|
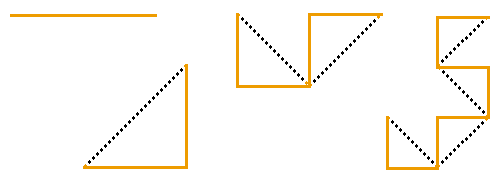  The corresponding curves, in order of complexity, are shown in the top diagram. The dotted lines indicate the curve at the previous level, turned through 45°. The level 14 curve is pictured above. |
||
| Further investigations
3. Look at the row entries f(n) in the dragon (or paper–folding) sequence corresponding to n = 4, 8, 12, 16, ... . What appears to be true? Can you prove it? |
7. Investigate the sequence a1, a2, a3, ... defined in the box below.
For example, starting with a1 = 24 we get 24, 12, 6, 3, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, ... . Try some other starting values and make a conjecture. This conjecture has never been proved! 8. A visual deficiency of our dragon curve is that it intersects itself. This can be avoided by rounding off the corners. For example, in the program we might replace ‘lt 90’ by ‘lt 45 fd X lt 45’ (where X is some small fixed distance), and similarly change ‘rt 90’. (This will slightly enlarge the drawn curve.) Try running the program with this modification. |
|