| Basic ideas
When we start learning geometry, it is almost axiomatic that: a straight line has dimension 1, But exactly what is this dimension? An intuitive idea is that the dimension corresponds to ‘the number of degrees of freedom’ the object has. This looks like replacing a hard idea with an even harder one! But perhaps we can best explain it using coordinates. The position of a point on a line can be given using just one coordinate – for example we might take the signed distance from the origin.
|
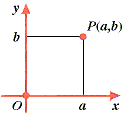 On the other hand, to describe the position of a point in the plane requires two coordinates – corresponding to two, generally perpendicular, axes. Similarly the position of a point in space can be described by three coordinates. On the other hand, to describe the position of a point in the plane requires two coordinates – corresponding to two, generally perpendicular, axes. Similarly the position of a point in space can be described by three coordinates.
It seems then that the dimension of an object can be defined as the number of coordinates required to specify the position of a general point of the object. Notice that in the case of a line, we do not require the line to be straight: for example, an arc of a circle has dimension 1. This seems to tie up the idea of dimension pretty well, but we are in for some surprises! |
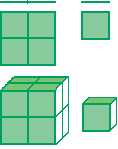
| A ball of twine
Consider now a ball of twine. We ask: what is the dimension of this ball? 1. (a) Think of looking at the ball from a distance. It appears to be a solid ball. What is its dimension? (b) Now look at the ball a little more closely. You can see that it is made up of twine – a line which is wrapped around and around. What is its dimension? (c) On closer inspection we see that the twine itself appears to be solid. What is its dimension? (d) Through a magnifying glass we see that the twine itself is made up of strands – each strand a line. What is the dimension here? |
(e) What do we see with the help of a microscope? Continue the analysis for several increasing powers of magnification.
It seems then that the dimension of an object may depend on the way we look at it. Perhaps dimension is not such a simple idea after all!
|
| The Peano curve
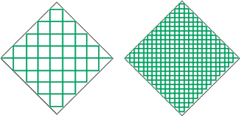
In 1890 Giuseppe Peano discovered the Peano curve. This curve has a new and very strange property: it actually fills a portion of the plane. For this reason it is sometimes called a space-filling curve. The initial line segment is replaced by nine smaller segments, as in the figure below. In the same way, each of these nine segments is then replaced with a further nine segments. At each level, the Peano curve is contained in a diagonal square, S, which is ultimately filled in. The Peano curves of levels 2 and 3 are illustrated. Peano showed that in the limit this curve passes through every point of S. So although it is a curve (of dimension 1?), it actually completely fills in region S (dimension 2). How can we resolve this dilemma? |
|||
|
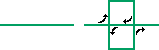  |
||
|
| Further investigations
4. A point is usually said to have dimension 0. Draw a point. Does it have length? breadth? What if you drew it very carefully? Must we distinguish between a drawn point and a mathematical (ideal) point? (The same argument applies to straight lines.)
|
7. (a) ‘Flatlanders’ are people who live in the plane. They can’t see ‘up’ or ‘down’. A sphere comes to visit them, and passes right through their plane. What do the Flatlanders see? (b) Could you define a 4-dimensional sphere? If a 4-dimensional sphere came to visit us, what would we see? (Would we believe it?!) |
|||||||||