|
||
 |
| The burden of proof
Suppose that after looking at a large number of examples, we arrive at the conjecture, ‘the sum of the first n odd numbers is n2’. How do we prove our conjecture, that is, how do we show that it is true for all values of n? We can certainly demonstrate that it is true for certain values of n, as follows:
1. Verify that the same pattern continues by filling in some more lines of the table. The numbers in the right-hand column are, indeed, the values of n2. Such a demonstration, however, comes nowhere near proving the truth of the conjecture for all values of n. No matter how many values of n we try, there will always be infinitely many untried values. Something more is needed. The technique of mathematical induction is useful for providing rigorous proof. |
|
|
||||||||||||
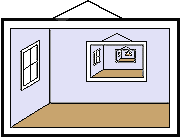 Recursion Recursion
An object is said to be recursive if it somehow contains a copy of itself. This picture, for example, is recursive because the picture hanging on the wall shows the room, including the picture hanging on the wall. Most of the fractals described in this book are recursive; they contain smaller copies of themselves. The procedures used to write them are also recursive; they contain calls to themselves. In theory, recursion goes on for ever. The above picture contains an infinite number of copies of itself. We cannot see them (and we do not have to draw them) because after a few levels they are too small to see. |
In practice, when we write recursive programs, we must limit the recursion by saying something like ‘if the shape is too small to see, go no further’. This is known as the ‘stop condition’, and such a condition must be part of every recursive procedure. Without a stop condition, a recursive procedure would never finish.
In the programs given here, recursion is generally controlled by the level of the fractal being drawn. If the level is 0, a simple, non-recursive, non-fractal shape is drawn. The level n fractal consists of several copies of the level n – 1 fractal, and the procedure calls itself to generate them. Do you see the similarity of this description to that of proof by induction? 4. Look back to the programs in previous sections. Which follow the pattern just described? How is the program for the dragon curve recursive? |
| The Sierpinski carpet |
|
|||
|
The Sierpinski carpet is similar to the Sierpinski sieve: the sieve is based on a triangle, the carpet on a square.
|
||||
|
The level 0 carpet is a square. We get the level 1 carpet by dividing the square into nine smaller squares, removing the central square (above). Thus we have eight copies of the level 0 carpet, arranged around a square.We get the level 2 carpet by repeating the same operation on these eight small squares, and so on. | |||
| The program draws a carpet of size 160 and level 4, with top-left corner at position (-80, -80) on the screen. The Square procedure draws a filled-in square at position (x,y) and with the given size. |  |
|||
|
The Carpet procedure is recursive. If level = 0, the stop condition, a call is made to Square to draw a filled-in square. If level > 0, the carpet is constructed by eight recursive calls to draw carpets of 1/3 the size, suitably positioned. |
||||
| The Menger sponge
5. Try some variations in the Sierpinski carpet program. For example, remove the corner squares, or the side squares, instead of (or as well as) the middle one. Try to predict what the fractal will be like before you run the program. The Sierpinski carpet can be extended into three dimensions to produce an object called the Menger sponge. The sponge is based on a cube. The Sierpinski carpet process is applied to each face of the cube. When a section of the face is removed, the removal is cut right through the cube. A Menger sponge of level 3 is illustrated – still, and animated. |
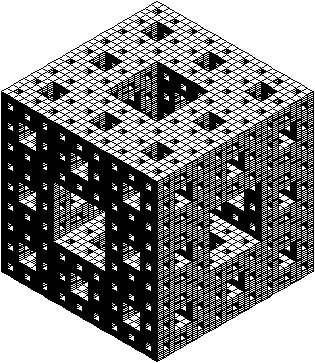 |
|
The term ‘sponge’ is often used for fractals which are full of holes but still connected in a single piece. The Sierpinski Carpet is a sponge in two dimensions. Other fractals comprise an infinite number of disconnected points, distributed in a fractal pattern. Such a fractal is called a dust. |
|
| Further investigations
6. How moth-eaten is the Sierpinski Carpet? What is the area of a carpet (of level infinity) with sides of length 1? 7. Calculate the volume of a Menger Sponge with edges of length 1. Do the calculation for sponges of level 0, 1, 2 and infinity. 8. Using the ideas discussed in Section 8, calculate the fractal dimension of the Sierpinski Carpet and the Menger Sponge. 9. We have seen how the Sierpinski Carpet can be extended into three dimensions to give the Menger Sponge. Can you visualize a three-dimensional extension of the Sierpinski Sieve? It might help to know that it is called the Sierpinski Tetrahedron. |
10. Examine some real sponges of different species. Do you think they have a fractal structure? How do they compare with a piece of foam rubber? Fractal geometry has in fact been used to simulate the growth of sponges and similar organisms.
|
|