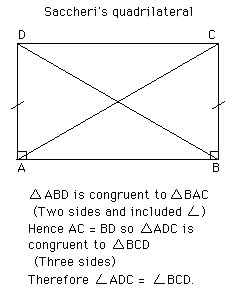
 The attempts continued, to try and prove the fifth postulate in terms of the other four. The first major breakthrough was due to Girolamo Saccheri in 1697. His technique involved assuming the fifth postulate false and attempting to derive a contradiction. What Saccheri found was as in the diagram, the summit angles ADC and BCD are equal. This gave three cases for him to consider, The attempts continued, to try and prove the fifth postulate in terms of the other four. The first major breakthrough was due to Girolamo Saccheri in 1697. His technique involved assuming the fifth postulate false and attempting to derive a contradiction. What Saccheri found was as in the diagram, the summit angles ADC and BCD are equal. This gave three cases for him to consider,
1. The summit angles are > 90 degrees
(hypothesis of the obtuse angle).
2. The summit angles are < 90 degrees
(hypothesis of the acute angle).
3. The summit angles are = 90 degrees
(hypothesis of the right angle).
Using Euclid’s assumption that a straight line is infinite, Saccheri managed to derive a contradiction for the first hypothesis and a hazy contradiction for the second one. Around 100 years later, Legendre also worked at the problem. He gave another equivalent statement to the fifth postulate, that is,
The sum of the angles of a triangle is equal to two right angles.
Using a similar idea to Saccheri, Legendre showed that the sum of the angles of a triangle cannot be greater than two right angles, however his proof rested on the assumption of infinite lines. Legendre also provided a proof on the sum not being less than two right angles, but again there was a flaw, in that he had made an equivalent assumption to the fifth postulate. |
 The attempts continued, to try and prove the fifth postulate in terms of the other four. The first major breakthrough was due to Girolamo Saccheri in 1697. His technique involved assuming the fifth postulate false and attempting to derive a contradiction. What Saccheri found was as in the diagram, the summit angles ADC and BCD are equal. This gave three cases for him to consider,
The attempts continued, to try and prove the fifth postulate in terms of the other four. The first major breakthrough was due to Girolamo Saccheri in 1697. His technique involved assuming the fifth postulate false and attempting to derive a contradiction. What Saccheri found was as in the diagram, the summit angles ADC and BCD are equal. This gave three cases for him to consider,