|
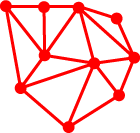
6. NON-SIMPLE LATTICE POLYGONS Euler and Pick Pick’s Theorem, as we have given it, applies to what are called simple polygons: polygons with a non-intersecting boundary which divides the planes into two regions – an inside (interior) and outside (exterior). We shall show that there is an extension of Pick’s theorem to a wider class of lattice polygons which we shall specify shortly. To understand this extension, we need to realize that there is an interesting connection between Pick’s Theorem and Euler’s Formula. Suppose we have a map made up of points (vertices) which are joined by (not necessarily straight) arcs (edges) in the plane which partition the plane into non-overlapping regions (faces). There are some constraints on this map: for example, we insist that the map have at least one point, be ‘in one piece’, that the map have no ‘loops’ (an edge with two endpoints in common), and that the edges do not cross (apart from meeting at a common endpoint).
Then for such a map having V vertices, E edges and F determined faces, V – E + F = 2 (Euler’s Formula). Thus for the map at left, above, V = 8, E = 11, F = 5 (including the exterior region) and V – E + F = 8 – 11 + 5 = 2 as required. Euler’s Formula is easily established by induction. It is clearly true for just one point (V = 1, E = 0, F = 1). Suppose it is true for some given map, and consider the effect of adding one further edge. Either such an edge joins an existing vertex to a new vertex (so V and E are each increased by 1, and the formula is unchanged), or it joins two existing vertices (in which case E and F are each increased by 1 and the formula is unchanged). Hence Euler’s Formula is true for all planar maps. We observe that this proof bears some similarity to the additive part of the proof of Pick’s Theorem: in each case, adding to the figure leaves the formula unchanged. Funkenbusch [F] established the connection as follows. Suppose we have a simple polygon with B boundary points, I interior points, and triangulate it completely to obtain E edges. Then we claim that Extending Pick’s Theorem We can extend Pick’s Theorem to cover non-simple polygons. We shall assume that for our non-simple polygon P, (a) if two edges of P intersect, their intersection is a vertex of each and so a lattice point; (b) every boundary point belongs to a non-degenerate lattice triangle which is contained in P; (c) the ‘area enclosed by P’ is the sum of the areas of regions which can be reached from ‘outside P’ by an odd number of crossings of the boundary (the shaded areas below).
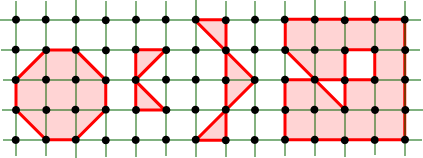
Now assuming that our polygon P has V vertices, E edges and F actual faces (that is, we don not count the exterior region), we define the Euler characteristic, We can now prove the Extended Pick’s Theorem The area of any lattice polygon is given by A(P) = 1/2B + I + k, where k = – Before we establish the theorem, check out the entries in this table which refer to the four polygons pictured above.
Notice that in Case (a) the value k = –1 gives the standard Pick Formula, as expected. Proof of the Extended Pick’s Theorem This clever proof appears in [GKW] and is quoted in Rosenholz [R]. Let P be our triangulated polygon, and let D be the ‘double’ of P : we form D by taking two copies of P and gluing them together along corresponding points of their boundaries. D is certainly a triangulated region: you might like to think of it as ‘inflated’ and lying on the surface of a sphere. We let the letters V, E and F denote the total number of vertices, edges, and faces (primitive triangles) respectively, and we use subscripts where necessary to distinguish between P and D. We now have
Now we put it all together. FD = = ( 2 = 2 = 2 Hence 1/2FD = 2 I + B – 2 and so A = 1/2FP by (6) = 1/4 FD by (5) = I + 1/2 B – as claimed. Rosenholz gives a discussion of the ‘obvious’ claim that primitive lattice triangles have area 1/2. Further result
Thus we obtain the interesting generalization of Pick’s Theorem: A = I + 1/2E – F. For simple polygons, E = B and F = 1, and we obtain the usual Pick formula. See Hadwiger and Wills [HW] (in German), and Rosenholz [R2]. [F] Funkenbusch, W. W., From Euler’s formula to Pick’s formula using an edge theorem, American Mathematical Monthly 81 (1974) 647 – 648. [GKW] Gaskell, R. W., Klamkin, M. S., Watson, P., Triangulations and Pick’s theorem, Mathematics Magazine 49 (1976), 35 – 37. [HW] Hadwiger, H., Wills, J. M., Neuere Studien über Gitterpolygone, Journal für die reine und angewandte Mathematik 280 (1973) 61 – 69. [R] [R2] Rosenholz, I., Calculating surface areas from a blueprint, Mathematics Magazine 53 (1979) 252 – 256. |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||