|
8. CENTRE OF GRAVITY Minkowski’s Theorem gives us an upper bound on the area for convex sets which are symmetric about the origin O and which contain no other points of the integer lattice. Are there other ways we can restrict our set in order to obtain a bound on the area?
Examples: The centre of gravity of a point-symmetric set is the centre of There is an interesting result about the centre of gravity called Winternitz’s Theorem. We won’t take time to prove it here, but a proof can be found in the nice book Convex Figures by Yaglom and Boltyanskii [YB]. Winternitz’s Theorem A convex figure is divided into two parts by a line which passes through its centre of gravity Then the ratio of the two parts lies between the bound 4/5 and 5/4.
Now, let us return to our lattices. Let K be a convex set which has its centre of gravity at the origin, O, and which contains no other point of the integer lattice. In 1955, French mathematician Eugene Ehrhart [E] found an upper bound for the area A(K).
|
|||||
You should have conjectured A
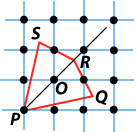
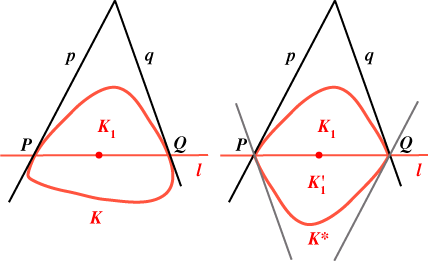
The proof of this theorem uses Winternitz’s Theorem, and is quite simple. Proof of Ehrhart’s Theorem Let K be a set as in the statement of the theorem. Choose a line l through the origin, dividing K into two parts, K1 and K2 say. Now let L meet the boundary of K in points P, Q. Let lines p, q through P, Q respectively be tangents to K. (If the boundary of K is not smooth at either of these points, take p, q to be ‘support lines’ to K. If p is a support line to K at P, it passes through P, and all points of K lie to one side of p or on p.) In either case, either p, q are parallel, or they meet, say on the K1 side of l. We now form a new set K* which is the union of K1 and its reflection K1' in the origin. This new set K* is convex, symmetric in the origin, and contains no other points of the integer lattice. We can thus apply Minkowski’s Theorem to it: A(K*) But by Winternitz’s Theorem, so A(K)
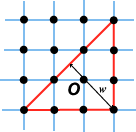
(1) Like Minkowski’s Theorem, Ehrhart’s Theorem generalizes easily to more general lattices L. The final statement becomes A(K) (2) A natural question to ask is whether Ehrhart’s Theorem generalizes to higher dimensions. In 1964 Ehrhart [E2] himself made the conjecture that in n dimensions, the volume V(K) of a convex body K with centre of gravity at O and containing no other lattice points satisfies V(K) (3) It is possible to use Ehrhart’s argument to some sets with centre of gravity not at the origin. For example, if the centre of gravity G of the planar set K does not lie at O, but the chord of K determined by G and O is bisected by O, and K contains no other points of the integer lattice, then A(K) (4) Here is another idea. The centre of gravity is a special point associated with the convex set K. What if we insist that some other special point of K lie at the origin? For example, the circumcentre of the planar set K is the centre of the unique smallest circle which contains K. Scott [S2] conjectures that a certain truncated triangle with circumcentre at the origin and containing no other lattice points has maximal area. The bound here is approximately 4.04, and the corresponding circumradius is approximately 1.637. Interestingly, I suspect that the irrationality of the bound here means that this is not regarded as an interesting problem! I’m not quite sure why this should be. (5) We could instead keep the centre of gravity condition and instead of asking for a bound on the area, ask for a bound on some other parameter associated with K. We shall look at the options in more detail in Chapter 9. However, the width w(K) of planar set K is defined to be the least distance between two parallel support lines. In 1982 I made the following conjecture: If the centre of gravity of planar convex set K lies at the origin, and K contains no further lattice points, then w(K)
[E] Ehrhart, E., Une généralization du théorème de Minkowski, Comptes Rendus, 240 (1955) 483 – 485. [E2] Ehrhart, E., Une généralization probable du théorème fondamental de Minkowski, Comptes Rendus, 258 (1964) 4885 – 4887. [E3] Ehrhart, E., Volume reticulaire critique d’un simplexe, Journal für die reine und angewandte Mathematik, 305 (1978) 218 – 220. [HCSG] Hernández Cifre, M. A., Scott, P. R., Gomis, S. S., On the centre of gravity and width of lattice constrained convex sets in the plane, Beiträge zur Algebra und Geometrie, 38 (2) (1997) 423 – 427. [S] Scott, P. R., Lattice points in convex sets, Mathematics Magazine, 49 (3) (1976) 145 – 146. [S2] Scott, P. R., Two problems in the plane, American Mathematical Monthly, 89 (1982) 460 – 461. [YB] Yaglom, I. M., Boltyanskii, V. G., Convex Figures, Holt, Rinehart and Winston (1961) |
|||
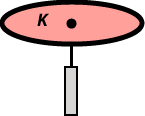 Suppose we have a finite planar set K. Think of the set K as being cut out of a piece of uniform card. Then the centre of gravity of K is the unique point of balance of the set: that is, the point of the set at which the card would exactly balance on the point of a needle. The centre of gravity can be defined (with difficulty) in a purely mathematical way.
Suppose we have a finite planar set K. Think of the set K as being cut out of a piece of uniform card. Then the centre of gravity of K is the unique point of balance of the set: that is, the point of the set at which the card would exactly balance on the point of a needle. The centre of gravity can be defined (with difficulty) in a purely mathematical way.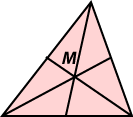 symmetry. The centre of gravity of a triangle is the centroid (the common point of trisection of the medians).
symmetry. The centre of gravity of a triangle is the centroid (the common point of trisection of the medians).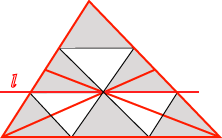
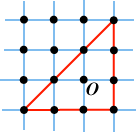 We see that equality is obtained (for example) for the illustrated right-angled triangle which has its centroid at O.
We see that equality is obtained (for example) for the illustrated right-angled triangle which has its centroid at O.