The Inventor
 James Watt was a Scotsman who lived from 1736 to 1819. He is remembered as the inventor and developer of the steam engine.
James Watt was a Scotsman who lived from 1736 to 1819. He is remembered as the inventor and developer of the steam engine.
 It is interesting that the whole theory of linkages really sprang from the industrial revolution. The steam engine utilized a piston which moved in an up and down motion. The photo at right shows a Watt steam engine in the Madrid museum. We can see the vertical piston at the left of the photo. Questions then naturally arose as to how best to translate this movement into circular motion, or how to translate circular motion into linear motion, or how to translate vertical linear motion into horizontal linear motion, and so on.
It is interesting that the whole theory of linkages really sprang from the industrial revolution. The steam engine utilized a piston which moved in an up and down motion. The photo at right shows a Watt steam engine in the Madrid museum. We can see the vertical piston at the left of the photo. Questions then naturally arose as to how best to translate this movement into circular motion, or how to translate circular motion into linear motion, or how to translate vertical linear motion into horizontal linear motion, and so on.
Why was this important? One practical reason at the time was the lack of precision engineering tools to produce straight metal slides which could guide a point along a straight line. This task presents very few problems today.
In 1784, Watts devised a linkage to which he gave the name ‘Parallel (straight line) motion’ which was included in an extensive patent. Years later he told his son: “Though I am not over anxious after fame, yet I am more proud of the parallel motion than of any other mechanical invention I have ever made.” A painting of him in the National Gallery in London shows him contemplating a drawing of this linkage.
 The Linkage
The Linkage
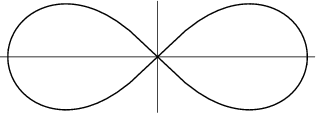
In its simplest form the linkage has three bars. The wooden model at left demonstrates how this linkage works Point A rotates on a circle centre D. Point B rotates on a circle centre C. Points A and B are joined by a link (of fixed length), and M is the midpoint of this link. As A (for example) is made to rotate about D, the point M traces out a ‘figure 8’ curve known as a lemniscate.
At this stage you may well wonder where the terms ‘parallel’ and ‘straight line’ come into play! Think of the linkage placed so that M is on the crossing point of the lemniscate. Also think of the piston of the steam engine being harnessed to the link AD, moving up and down to cause a small backwards and forwards circular motion of the link. This causes point F to move backwards and forwards over a small, almost straight portion of the lemniscate. The motion of the piston and the movement of point F can easily be made parallel by suitably positioning the linkage.
Sometimes this linkage is described as one which converts circular motion to (approximate) linear motion. This is clearly the case: we just have to start with the rotating link AD.
Over time, various refinements of this linkage were made.
 The Mathematics
The Mathematics
Jakob Bernoulli published an article in Acta Eruditorum in 1694 in which he called this curve the lemniscus (Latin for ‘a knot, or bow of ribbon’). The general properties of the lemniscate were investigated by Fagnano in 1750. Later, Gauss and Euler tried to find the arc length of the curve; this led to later work on elliptic functions.
The lemniscate is not a particularly easy curve to study. Let F(– a, 0), F'(a, 0) be two fixed points, called the foci of the curve. Then the lemniscate is the locus of points P(x, y), for which PF.PF' = a2. This gives the Cartesian equation
{(x + a)2 + y2}.{(x – a)2 + y2} = a4
where both sides of the equation have been squared. Expanding and simplifying then gives
(x2 + y2)2 = a2(x2 – y2).
The curve has polar equation: r2 = a2cos 2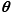 .
.
The Java Applet
Since this is such a simple linkage, let us try some refinements of our own! We shall add some segments which allow us to vary the lengths of the individual links.
I had such a lot of fun creating this applet. Of course it evolved gradually. Starting with the basic linkage, I soon discovered that I obtained half a lemniscate bounded by a semicircle, so adding a reflection was a good idea. Then, what about control buttons? And some way of altering the length of the links?
The JSP window is 300 wide and 350 high. I have taken AB = 100, and initial values of AP = BQ =70, PQ = 100.
If after creating your own applet, you want to check your construction code, click here.
|
|
 James Watt was a Scotsman who lived from 1736 to 1819. He is remembered as the inventor and developer of the steam engine.
James Watt was a Scotsman who lived from 1736 to 1819. He is remembered as the inventor and developer of the steam engine.  It is interesting that the whole theory of linkages really sprang from the industrial revolution. The steam engine utilized a piston which moved in an up and down motion. The photo at right shows a Watt steam engine in the Madrid museum. We can see the vertical piston at the left of the photo. Questions then naturally arose as to how best to translate this movement into circular motion, or how to translate circular motion into linear motion, or how to translate vertical linear motion into horizontal linear motion, and so on.
It is interesting that the whole theory of linkages really sprang from the industrial revolution. The steam engine utilized a piston which moved in an up and down motion. The photo at right shows a Watt steam engine in the Madrid museum. We can see the vertical piston at the left of the photo. Questions then naturally arose as to how best to translate this movement into circular motion, or how to translate circular motion into linear motion, or how to translate vertical linear motion into horizontal linear motion, and so on. The Linkage
The Linkage The Mathematics
The Mathematics