4. CHEBYSHEV LINKAGE

The Inventor

Pafnuty Lvovich Chebyshev (or Tchebicheff) lived from 1821 until 1894. He was a Russian mathematician who founded of the St. Petersburg Mathematical School, and is remembered for his work on prime numbers and probability. He studied theoretical kinematics, particularly rectilinear motion.

Chebyshev was a prolific mathematician. In number theory, he worked on the distribution of prime numbers. He then turned to applied mathematics and began a lengthy study of mechanical systems. Besides inventing a number of mechanical linkages, he also developed techniques of numerical analysis for dealing with theoretical calculations in mechanics. He later tackled the fields of probability and statistics, proving important basic theorems including the law of large numbers.

Judging by his published works and his reputation abroad, his interest in kinematics and linkages amounted to an obsession. In 1853, after visiting France and England and observing carefully the progress of applied mechanics in those countries, he wrote his first paper on approximate straight-line linkages, and over the next 30 years he attacked the problem with new vigor at least a dozen times.

Chebyshev is considered a founding father of Russian mathematics. According to the Mathematics Genealogy Project, Chebyshev has about 5,000 mathematical ‘descendants’.
The Chebyshev crater on the Moon and the asteroid 2010 Chebyshev were named in his honour.

The Linkage

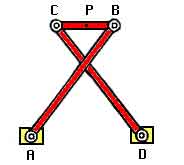The Chebyshev linkage is a mechanical linkage that converts rotational motion to approximate straight-line motion. In the figure at right, A, B are fixed pivots. C and D are moveable pivot points, and P is the midpoint of CD. Rotation of B through a circular arc about A results in an approximate linear movement by P. The proportions used in this linkage are AD : BC : AB (= CD) = 2 : 1 : 2.5. This relationship assures that the links AB, CD lie vertically when they are at the extremes of their movement.


The Mathematics

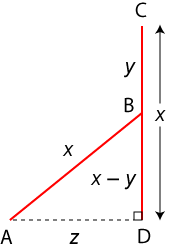Suppose we set AB = CD = x, BC = y, and AD = z.

Then we are given that x : y : z = 2.5 : 1 : 2.
This means we can write x = 2.5y, z = 2y.

Now by placing the linkage in one of its extreme positions with BC, DC vertical and overlapping, we easily obtain

                                   x – y = 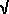(x² – z²).

Notice by substituting that this checks with the assumed ratios of the link lengths.

The point P (the midpoint of BC) in this position lies x – y/2 = 2y above AD, and the same holds when P lies directly above point A.

When P lies above the midpoint of AD, the linkage is then in the position shown in the top linkage diagram, and using the right triangle with AB as hypotenuse, we see that BC (and so P) is a distance 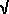(6.25y² – 9y²/4) = 2y above AD. This gives three positions of P on this straight line.

Since we expect the locus of P to only only approximately straight, I suspect a numerical plotting of the locus might be the best approach from here.

The Java Applet