The Inventors
Charles-Nicolas Peaucellier lived from 1832 to 1913, and was a French army officer. Lippman Lipkin lived in Lithuania. These two inventors independently discovered the linkage which bears their names, the Peaucellier – Lipkin linkage (or Peaucellier – Lipkin cell), which was invented in 1864. This was the first linkage capable of transforming rotary motion into perfect straight-line motion, and vice versa. Its invention was noteworthy because people were beginning to think that designing a linkage to convert circular to linear motion was not possible. A previous attempt by Watt only yielded an approximatuion to straight line morion.
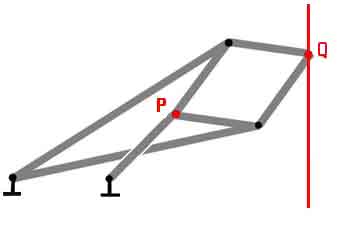 The Linkage
The Linkage
The Peaucellier – Lipkin linkage is illustrated at right. The point P is constrained to move in a circle about a fixed pivot. As this occurs, rather surprisingly the point Q traces out a straight line.
The Mathematics
The Peaucellier – Lipkin linkage is directly related to a gemetric transformation known as inversion in a circle, which transforms the plane into itself. (Strictly, there is a problem with the centre of the circle!)
Suppose we are given a fixed circle C of radius r in the plane, centred at the origin O. Then under inversion in C, any point P in the plane other than the center O of C, transforms to point Q where P and Q are collinear with O and further:
OP x OQ = r2
Among the many remarkable features of this transformation is that it maps circles and lines to circles and lines. In particular, if a circle passes through the centre O of the fixed circle, then inversion maps this circle into a straight line.
Now let’s see what needs to be proved. In the geometric diagram of the apparatus (below), six bars of fixed length can be seen: OA = OC, AB = BC = CD = DA. Also, point O is fixed. Then, if point B is constrained to move along a circle (shown in red) which passes through O, then point D will necessarily have to move along a straight line (shown in blue). On the other hand, if point B were constrained to move along a line (not passing through O), then point D would necessarily have to move along a circle (passing through O).
We need to prove three results:
• Points O, B, D are collinear.
• Points B and D are inverse points.
• If the locus of B is a circle through O, then the locus of D is a straight line.
We could establish the collinearity of points O, B, D by rather pedantically introducing the centre P of the rhombus and then showing corresponding triangles above and below OD are congruent. However, we are probably prepared to accept this result as a consequence of the symmetry of the figure.
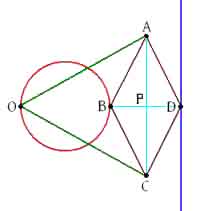 The inverse property is the more interesting.
The inverse property is the more interesting.
Let point P be the intersection of lines AC and BD. Then, since ABCD is a rhombus, P is the midpoint of both BD and AC. Hence length BP = length PD. Furthermore ir is well known (and easily proved) that the diagonals of a rhombus intersect at right angles.
Now set x = BP = PD, y = OB, and h = AP.
Then:
OB.OD = y(y + 2x) = y2 + 2xy
OA2 = (y + x)2 + h2 (by Pythagoras)
AD2 = x2 + h2 (by Pythagoras)
OA2 – AD2 = y2 + 2xy = OB.OD.
Since OA and AD are both fixed lengths, then the product of OB and OD is a constant:
OB.OD = k2 (say).
Since points O, B, D are collinear, then D is the inverse of B with respect to the circle with center O and radius k.
Finally, using the properties of inversion, point B traces out a circle through the centre of inversion if and only if point D traces out a straight line not through O. You can find a proof of this at:
http://internal.maths.adelaide.edu.au/people/pscott/PLC/12/12.html
Although linkages as a subject went well beneath the radar of the mathematics community for some time, interest in these problems has been rekindled by new developments in engineering (robotics) and computer science.
The Java Applet
At right is the applet we will construct.
This applet is fairly straightforward. The image of the circle traced out by the red driver point is in fact mathematically the whole of the blue line. The reason the whole line does not appear here is a failing of the linkage method of construction.
I have chosen A and B to be 50 pixels apart, the short segments 60 pixels, and the long segments 140 pixels. The rectangle is 330 x 310 pixels.
To see my applet code, click here.
|
|
 The Linkage
The Linkage The inverse property is the more interesting.
The inverse property is the more interesting.