|
Gauss (1777 – 1855) found that a regular polygon having n sides can be constructed using just straightedge and compass if the odd prime factors of n are distinct Fermat primes, that is, prime numbers of the form 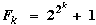 . The only known primes of this kind are F0 = 3, F1 = 5, F2 = 17, F3 = 257 and F4 = 65537. The regular 257-gon was constructed in 1832. The mathematician J. Hermes spent ten years constructing the regular 65537-gon, and deposited the manuscript in a large box in the University of Göttingen where it may still be found! . The only known primes of this kind are F0 = 3, F1 = 5, F2 = 17, F3 = 257 and F4 = 65537. The regular 257-gon was constructed in 1832. The mathematician J. Hermes spent ten years constructing the regular 65537-gon, and deposited the manuscript in a large box in the University of Göttingen where it may still be found!
|
|
 It follows that the first few regular polygons of n sides which can be constructed with straightedge and compass are those with n = 3, 4, 5, 6, 8, 10, 12, and 15. Of course the architect of Hauterive would not have known of Gauss’s result. However, it is more than likely that he was aware of Euclid’s Elements, and in particular Book IV in which Euclid discusses how to inscribe a regular n-gon in a circle for n = 3, 4, 5, 6, and 15. It follows that the first few regular polygons of n sides which can be constructed with straightedge and compass are those with n = 3, 4, 5, 6, 8, 10, 12, and 15. Of course the architect of Hauterive would not have known of Gauss’s result. However, it is more than likely that he was aware of Euclid’s Elements, and in particular Book IV in which Euclid discusses how to inscribe a regular n-gon in a circle for n = 3, 4, 5, 6, and 15.
Strangely, window XVIII gives an implicit 9-gon. However, the window contains the numbers 3 and 5. Perhaps the designer was reaching for the 15-gon? Or just creating a beautiful design?! In any case, Hauterive is a fine example of the interplay between mathematics and architecture.
|