DODECAHEDRON + ICOSAHEDRON COMPOUND

    Dodecahedron and icosahedron

If we construct the dual of a cube by constructing the mediators of the edges, we obtain an octahedron. The two solids fit together in a nice symmetric way as shown.

Dodecahedron

Icosahedron

     

• (a) Make a table of the numbers V, E and F of vertices, edges and faces of the red dodecahedron.

V	E	F

    (b) Now make a table of the numbers V_D, E_D and F_D of vertices, edges and faces of the grey dual solid (icosahedron).

VD	ED	FD

    (c) As before, by setting up a correspondence, can you explain why the numbers in (b) occur?

We notice that in the construction

•  the number of red edges is the same as the number of grey edges, since there is a one-to-one correspondence between them;
•  the number of red vertices is the same as the number of grey faces, since a red vertex pyramid sits on each grey face;
•  the number red faces is the same as the number of grey vertices, since each red face acts as a base plane for a grey vertex pyramid.

The above argument shows that here we logically expect V = F_D, E = E_D, and F = V_D. We say that the dodecahedron and the icosahedron are dual polyhedra. We can write: the dual of {5, 3} is {3, 5}, and conversely.

The illustrated polyhedron is called the dodecahedron + icosahedron compound.  It is the compound of a dodecahedron and its dual, a regular icosahedron.

• In this compound polyhedron, does Euler’s formula hold? Looking at the diagram above (or the frame version of the applet below), calculate or count the number of vertices, edges and faces. Notice that these numbers are different from just adding the corresponding V, E and F for the two solids. Fill in the following table:

V	E	F	V – E + F

Now check your answers.

As previously, we can illustrate the relationship between the duals by placing one solid inside the other, matching the vertices of the inside polyhedron with the centres of the faces of the enclosing solid.

          

  Making the model

This compound also makes an attractive model.  For nets and instructions on making this model, check out this link.

  Playing with the applet

Once more, spend some time playing with the applet, and enjoying this beautiful compound polyhedron. Use the applet to check out the following statements:

• This compound can be viewed as a (regular) pentagon inscribed in a pentagon, lying inside a pentagon inscribed in a regular decagon.

• This compound can be viewed as an equilateral triangle inscribed in an equilateral triangle, lying inside a regular hexagon.

Check your answers ...




  Vertex coordinates

Suppose you want to construct a computer model of this compound. You will need a set of coordinates for each of the vertices.

•  (a) Give a set of coordinates for the 20 dodecahedral vertices.
    (b) Give a set of coordinates for the 12 icosahedral vertices. Can you use both sets together?
    (c) Calculate the coordinates of the 30 vertices occurring as the edge midpoints.

Now check your answers ...

From the construction of this compound, we can use our previous coordinates for the dodecahedron:

(1, 1, 1),   (0, ^–1, ),  (, 0, ^–1),  (^–1, , 0),

and icosahedron:

(, 1, 0), (0, , 1), ( 1, 0, ).

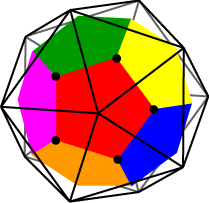
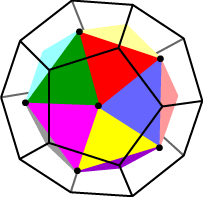
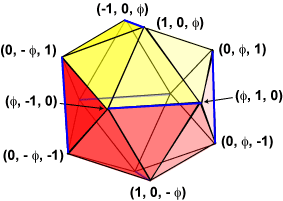The remaining 30 vertices of the compound are the edge midpoints of (say) the icosahedron. From the figure, we see that these will be:

   midpoints of the six blue segments:         

(, 0, 0), (0, , 0), ( 0, 0, );

   midpoints of the 24 segments with endpoints ( 1, 0, ), (0, , 1) and similar:           

 (1, , 1 + ), (1 + , 1, ), (, 1 +, 1).

Notice that we have expressed 30 = 3 x 2 + 3 x 2³.

You might also like to check that each of these midpoints is distant from the origin O.

  Real life occurrences

Here are some attractive occurrences of the dodecahedron plus icosahedron compound.

Example 1
Example 2
Example 3
Example 4

  References