|
FIVE OCTAHEDRA COMPOUND
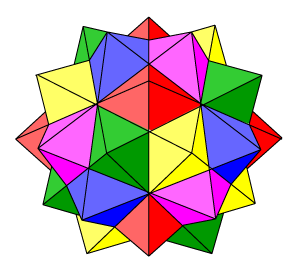
Our last compound in this section is the compound of five octahedra. Personally, I find this the least attractive of these compounds – rather like some sort of knobbly fruit! Nevertheless, it has some interesting structure. It occurs as the dual of the five cubes compound. The correspondence is: five cubes inscribed in a dodecahedron five octahedra intersecting in an icosahedron. As before, we can break this model down into its five component parts. Seeing the individual octahedra is really quite simple. Far more difficult is removing the octahedra one by one, and viewing the remains of the solid left behind. This is extraordinarily challenging to do, and I recommend this exercise to anyone wishing to improve their spatial understanding of this (and the other) compounds. So let us remove the octahedra one by one:
There are five octahedra in this compound, and each octahedron has eight faces. In the model, these faces occur in pairs in 20 planes, which enclose a regular icosahedron. A plane containing a blue triangular octahedral face and a magenta triangular octahedral face can be seen here. In the centre of the figure is an equilateral triangle which is a face of the enclosed icosahedron.
The convex hull of the five octahedra (i.e. the smallest convex set containing the octahedra) is a solid called an icosidodecahedron.
To make this model, check out this link. The 30 vertex pyramids are individually assembled, and then glued together. Although the resulting model is not quite rigid, it is satisfactory at normal display sizes.
Bob has created an amazing applet here – one which allows us to understand how this compound polyhedra is constructed about a regular icosahedron.
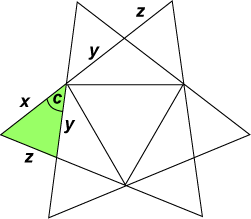
We have already seen that each planar face of this compound contains two equilateral triangles which are faces of the octahedra.
We have already seen that each planar face of this compound contains two equilateral triangles which are faces of the octahedra.
Hence, in the five octahedra compound, there is another triangular face in the plane of the red triangle, and these two coplanar triangles together are congruent to the (blue) triangular coplanar faces occurring with the ten tetrahedra compound. That is, as we saw before, they are angled at
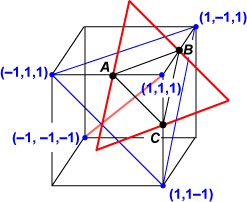
x + y + z = 1. The actual values of x, y and z are given on the MathWorld site listed below. A suggested approach would be to determine one of the remaining triangle angles using the (3-dimensional) coordinates of the triangle vertices, and then use the sine rule for the triangle. MathWorld: http://mathworld.wolfram.com/Octahedron5-Compound.html Cundy, H. M., Rollett, A. P., Mathematical Models, Oxford (2nd Edition 1961) Wenninger, M. J., Polyhedral Models, Cambridge (1971) |
The icosahedron has 20 faces. Each face of the icosahedron lies in two faces of the compound. This gives a total count of 40 faces.
Since each octahedron ha eight faces, 40/8 = 5 : the number of octahedra in the compound.
Obtaining these numbers is getting a little more tricky. |