|
FIVE TETRAHEDRA COMPOUND
We have seen how it is possible to inscribe a cube inside a dodecahedron, and also how it is possible to inscribe two tetrahedra inside a cube. If we choose just one of the inscribed tetrahedra from each cube in a consistent way, we get this very pretty compound of five tetrahedra. One of the attractions of this compound is that it has a definite orientation. If we look at one of the inner ‘dimples’ we see a clockwise(?) swirl of faces. The compound made from the other five tetrahedra has the swirl in the opposite direction. Each is the mirror image of the other, and the pair are said to be enantiomorphic. They are pictured below. Five tetrahedra have 20 vertices; a dodecahedron has 20 vertices. Hence using the symmetry of the compound, each vertex of the dodecahedron occurs as the vertex of just one tetrahedron. View this structure. We can break the model down into its five component tetrahedra. Another way of viewing the compound is to remove the cubes one by one:
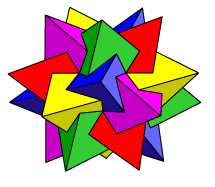 A pair of enantiomorphic solids A pair of enantiomorphic solids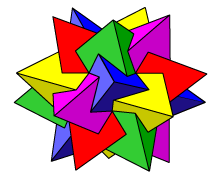
Let us look at the red face, and the lines on this face formed by the intersecting faces. We get a figure which looks like this. The lines on this face determine an equilateral triangle. Since there are 20 triangular faces, there are 20 such equilateral triangles. These triangles form the faces of an icosahedron, which is the solid of intersection of the five tetrahedra. We now show that each of the dimples of this compound occurs as the common intersection point of five diagonals of the defining dodecahedron. We shall need to use coordinates to do this, but the results are very pretty.
Using our knowledge of the defining dodecahedron, we can assign coordinates as follows:
We seek the coordinates of the dimple X.
This is a very pretty model to make, and well worth the effort involved. For instructions on preparing and assembling the pieces, check out this link.
It is profitable to spend some time playing with the applet, and enjoying this beautiful compound polyhedron. Use the applet to check out the following statements:
We have previously determined that the 20 vertices of the dodecahedron can be taken to be: (
The solution to (a) is straight-forward. We note that the distance between vertices is 2 (1, 1, 1), (1, –1, –1), (–1, 1, –1), (–1, –1, 1) and (–1, –1, –1), (–1, 1, 1), (1, –1, 1), (1, 1, –1);
Now to choose from these a suitable set of five tetrahedra, we simply avoid choosing any two tetrahedra having a common vertex. We thus obtain, for example: (1, 1, 1), (1, –1, –1), (–1, 1, –1), (–1, –1, 1); References MathWorld: http://mathworld.wolfram.com/Tetrahedron5-Compound.html Construction: Cundy, H. M., Rollett, A. P., Mathematical Models, Oxford (2nd Edition 1961). Wenninger, M. J., Polyhedron Models, Cambridge (1971). |
| (a) The green plane passes through the points (–1, 1, 1), (1, –1, 1), (1, 1, –1) and so has equation x + y + z = 1. You can check that G lies on this plane too, as do K and L (the green/blue and green/yellow intersection lines).
(b) FG is a diagonal of the dodecahedron, as is each of the five lines determining the dimple. (c) Solve u(–1, 1, 1) + (1 – u) ( (d) The ‘standard’ coordinates are obtained by scaling the inside polyhedron by |
