TEN TETRAHEDRA COMPOUND

             

   Putting it together

We have seen earlier how five tetrahedra can be inscribed in a dodecahedron, and in fact, in two enantiomorphic ways. The compound of ten tetrahedra arises when we build a compound of all ten of these tetrahedra. We can still see how they are inscribed in a dodecahedron. However, the model itself looks quite different. It is made up of 12 pentagonal star shaped dimples, which are connected around the edges by quadrilateral grooved indentations. As might be expected, the detailed structure is quite difficult, and the figure on the right above indicates how the faces lie on different intersecting planes.

  Intersection and structure

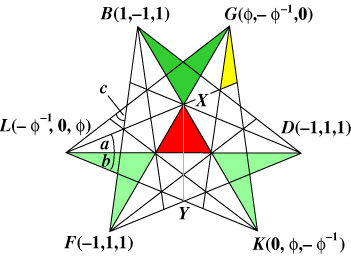
If we look for example at the blue plane in the figure at right, we obtain an outline together with intersecting lines. The outline appears to be two equilateral triangles placed asymmetrically. Why should this not surprise us?

Remember in our five-tetrahedra investigation, we found that the plane determined by

F (–1, 1, 1), B(1, –1, 1), D(1, 1, –1),

also passed through G(, ––1, 0), L (––1, 0, ), K (0, , ––1). The three points F, B, D determine an equilateral triangle of side length 22.

• What can you say about the three points G, L, K?

Check your answer.

Let us now look more closely at this two-triangle outline. We have added the above labels and coordinates. The easiest way to calculate some of the angles in this figure is to use the well-known:

                                                                                                                  

••••••••••••••• Cosine Rule •••••••••••••••

If is the angle between vectors u and v then
the dot product of the vectors satisfies u.v = |u|.|v| cos .
Knowing information about u and v can now give us the value of .

••••••••••••••••••••••••••••

• (a) Use your knowledge of the vectors BF and LG to find the angle c.

(b) Use your knowledge of the vectors LD and LK to find the angle b.

(c) Noting that the two defining equilateral triangles have common centroid (1/3, 1/3, 1/3), use the symmetry of the figure to show that LXDY is a rhombus, and so a = b.

(d) There are many parallel lines in this figure. You should now be able to see directly that c = a + b (= 2a).

Check your answers ...

Since there are ten tetrahedra, each having four faces, there are a total of 40 faces. However, as we have seen, these occur in pairs in common planes. Hence there are just 20 defining planes for this solid. These planes determine an icosahedron of intersection, one face of which is shown by the red equilateral triangle.


  Making the model

This is a comparatively simple model to make, considering the complexity of the solid. For instructions on preparing and assembling the pieces, check out this link. If you wish to make a model with the defining planes coloured individually, you will need to work this out before glueing and assembling, as it is very difficult to paint inside the grooves between the pentagonal dimples. Wenninger gives a colour pattern for one extended dimple. Altogether, you will need 20 different colours, or you might make do with just 10, using the same colour for parallel ‘opposite’ planes. Alternative colourings are much easier and very effective!


  Playing with the applet

It is profitable to spend some time playing with the applet, and enjoying this beautiful compound polyhedron. Use the applet to check out the following statements:

• The compound consists of 12 joined star dimples.

• The compound can be described as consisting of 20 overlapping tri-propellors.

• The compound can be views lying within a regular dodecagon with five diagonals through the centre.

• The compound has 20 planar faces each containing two overlapping triangles.


  Vertex coordinates

We have already done the hard work for finding the vertex coordinates, In the five-tetrahedra case, we found the vertex sets:

(1, 1, 1), (1, –1, –1), (–1, 1, –1), (–1, –1, 1);  
(–1, –1, –1), (0, – –1, ), (, 0, – –1 ), (– –1, , 0);
(–1, 1, 1), (0, –1, –), (, 0, –1 ), (– –1, –, 0);
          (1, –1, 1), (0, – –1, –), (–, 0, –1 ), ( –1, , 0);    and
(1, 1, –1), (0, –1, ), (–, 0, – –1 ), ( –1, –, 0). 

For the other tetrahedra, we use the remaining sets:

  (–1, –1, –1), (–1, 1, 1), (1, –1, 1), (1, 1, –1);      
(1, 1, 1), (0, –1, –), (–, 0, –1 ), ( –1, –, 0);
 (1, –1, –1), (0, – –1, ), (–, 0, – –1 ), ( –1, , 0);     
(–1, 1, –1), (0, –1, ), (, 0, – –1 ), (– –1, –, 0);  and
(–1, –1, 1), (0, – –1, –), (, 0, –1 ), (– –1, , 0).    

  References

MathWorld: http://mathworld.wolfram.com/Tetrahedron10-Compound.html

Construction:

Cundy, H. M., Rollett, A. P., Mathematical Models, Oxford (2nd Edition 1961).

Wenninger, M. J., Polyhedron Models, Cambridge (1971).

(a) As a vector, BF = (2, –2, 0) and GL = ( + –1, – –1, –).

Using the cosine formula, we obtain

cos c = 1/22 . 1/22 . [2( + –1) + 2–1 + 0] = 1/8.(6 – 4).

Using a calculator, c = 44.4775° = 44° 28'.

(b) Similarly, b = 22.2387° = 22° 14'.

(c) By symmetry, XY and LD are perpendicular bisectors, so LXDY is a rhombus. Hence a = b.

(d) In particular notice the parallel through G to BF. Using the angle measures a, b at G we easily see that c = a + b.

  They also form the vertices of an equilateral triangle of side length 22.