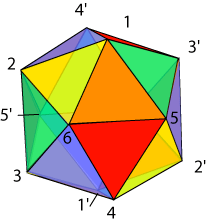
|
GREAT ICOSAHEDRON, {3, 5/2} or (3)5/2
This is a beautiful polyhedron, but its structure is quite complex and hard to come to terms with. First observe that the polyhedron is inscribed in a regular icosahedron. This solid is in fact a stellation of the icosahedron – according to Wenninger, the sixteenth stellation! Notice that the faces here are intersecting equilateral triangles. These are inscribed in the enclosing dodecahedron, and occur in parallel pairs. Here are some examples: Notice what happens here. In the icosahedron, opposite triangular faces lie in parallel planes, and each is related to the other in its orientation by a half turn. In the great icosahedron, correspondingly, there are two parallel triangular faces, each related to the other in orientation by a half turn. If you look carefully at the above figure, you will notice that as well as triangular faces, there are also many regular pentagrams. These are not faces: they are induced sets of edges, with each edge occurring as the intersection of two triangular faces. Each vertex of the solid protrudes from the centre of one of these pentagrams. We are now going to determine the number of vertices, edges and faces. As before, it is the whole triangles that make up the faces here, not the individual parts. Similarly, the vertices of the solid are where the (five) vertices of the triangle faces meet. And the edges are the long line segments joining the vertices.
Since each triangular face corresponds to a face of the icosahedron, F = 20. And since the vertices coincide with the vertices of a regular icosahedron, the number of vertices of this solid is 12. For the edges, each of the 20 faces has three edges, giving a count of 3 x 20; since each edge is counted twice in this calculation, we deduce that E = 30. Again, the Euler number 2 reappears here.
the great stellated dodecahedron {5/2, 3), and the great icosahedron {3, 5/2}. It is possible to construct a compound model of these two polyhedra, as at right. This shows the correspondence between the vertices of the great icosahedron, and the pentagonal star faces of the great stellated dodecahedron.
As with the Platonic solids, we can use this Java applet to play with each of the Archimedean solids. Use the applet to try to gain an understanding of the inter-relationships between the different parts of this fascinating solid.
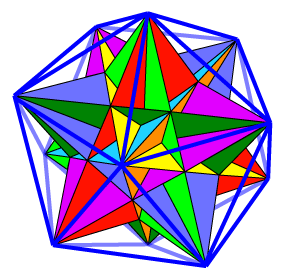
The most obvious way of colouring this solid is to use ten colours, one colour corresponding to each pair of parallel faces of the circumscribing icosahedron. Another suggestion is that made by Wenninger, of a colouring using just five colours. In either case, when making the model, we are faced with the difficult task of deciding how the facets are to be coloured on the net. We tackle here the more difficult five-colour option. The analysis will probably help our understanding of the structure of the great icosahedron itself. It arose because in my edition of Wenninger, there is a simple typo, but more importantly, the colours of the dimple triangles are omitted. To my slight embarrassment, these dimple triangles turn out to have the same colour as the triangle to which they are attached.
We can first list the defining planes and their colours. Entries in the final two columns are for the faces opposite to those in the first two columns.
To further understand the colouring, we notice that each vertex is set in a pentagonal dimple. We seek to define in order the colours of the planes defining each vertex and its surrounding dimple. The dimple faces are easy. Taking vertex 6 as an example, we see that in the original icosahedron, this vertex is surrounded by a pentagonal pyramid with base 12345(1) and vertex 6. In the great icosahedron, vertex 6 is surrounded by pentagram 13524(6). By the method of construction, the colours correspond in a simple way: for example the orange 156 face of the icosahedron gives rise in the great icosahedron to the orange inward facing 24 face of the pentagram about vertex 6.
Thus for the great icosahedron, we have the following colouring of the dimples. The edge notation can be thought of as directed: moving in the indicated direction implies that the stated colour is on the left. For example, moving from 2 to 5 gives the red colour to the left of the path.
Now let us try to find the ordered colours for the triangles around each vertex. Each vertex is the meeting point of five pentagrams. We list just the pentagram edges from a given vertex, repeating each. Notice that we can obtain the end vertices from the Schlegel diagram of the icosahedron by starting with the given vertex and ‘crossing two triangles’. We label each of the two edges at each vertex in the order they would appear by traversing the pentagram in an anticlockwise direction. Notice that the final six rows are obtained from the first six by reversing the order of the entries and dashing the components. Since by our labelling we have paired the ‘inner faces’ of the pentagrams, we can now add the colours from the above table.
Finally, let’s try to put it all together. Here are pyramid nets for the vertices, all in colour. The information comes from the above two tables.
After all this, I really prefer the ten colour colouring! The above colouring does achieve five colours around each vertex, but around the dimples you obviously get adjacent faces having the same colour.
The model of the small stellated dodecahedron is easy to make. See this construction page for some details.
It is a simple matter to derive a set of vertex coordinates for the great icosahedron. For, as we have seen, these vertices are just the vertices of a regular icosahedron. Hence from our previous work, we can take the 12 vertex coordinate sets to be:
MathWorld : http://mathworld.wolfram.com/GreatStellatedDodecahedron.html Wikipedia : http://en.wikipedia.org/wiki/Great_icosahedron
Cundy, H. M., Rollett, A. P., Mathematical Models, Oxford (1962). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Definition and notation
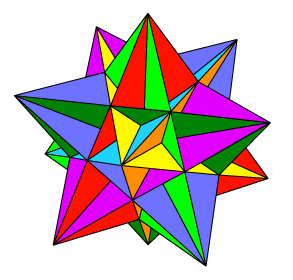The last of the four Kepler-Poinsot polyhedra is the great icosahedron, illustrated at right. It has intersecting triangular faces (indicated by the ‘3’ in the symbol), and each vertex figure is a regular pentagram {5/2}.
We observe that the great stellated dodecahedron has V = 20, E = 30, F = 12, while the great icosahedron has the dual values 
, 