|
DODECAHEDRON {5, 3}
At right is the Schlegel diagram for the dodecahedron. Does it have the right number of vertices, edges All the usual measurements can be calculated by the enthusiastic: surface area, volume, inradius, midradius, circumradius, dihedral angle. There seems to be no great merit in doing this; why not just read how someone else did it?! Here ...
The dodecahedron has a number of interesting properties. We shall use our applet to investigate some of these.
The cross-sections make us work rather harder. Working from a model (if you have one) is probably easier than working from the applet.
Then below are diagrams showing the regular cross-sections. It is perhaps surprising that we can obtain so many. The blue pentagonal section is of course no surprise, as each face of the dodecahedron is a regular pentagon. We can obtain a ‘proper} section by taking a parallel plane which cuts the solid. The magenta decagonal section is obtained by cutting the solid suitably through its centre. Is the green section actually square? The edge lengths are all equal (diagonals of congruent faces), so it must be at least a rhombus. Further, since the faces are congruent and regular, the two diagonals of the faces with a common edge are both ‘centred’ with respect to that edge. So the green section is a square. The factor of 3 in the triangular and hexagonal sections seems a little out of place, except that we have three faces meeting at each vertex. So the equilateral triangle section is just a vertex figure of the solid. Notice that the two regular hexagonal sections are different in nature: the orange section has vertices at edge midpoints, but the purple section has to have its vertices at carefully chosen points on the edges of the dodecahedron. My calculation shows that such points have to be at a ratio of
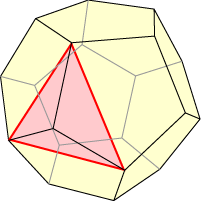
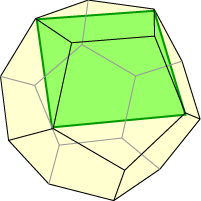
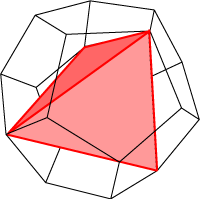
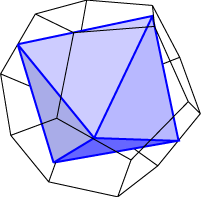
You might remember how we inscribe a tetrahedron inside a cube. We could now ask whether it is possible to inscribe a tetrahedron, a cube, or an octahedron nicely inside a dodecahedron.
Below are diagrams showing that each of these inscribed polyhedra exists. You might like to ask how many of each type of polyhedra can be inscribed in a given regular dodecahedron. We shall come back to this later.
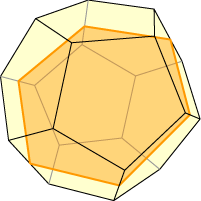
In the case of the dodecahedron inscribed in the cube, we notice that the dodecahedron has three pairs of mutually orthogonal edges. These edges can be placed in the faces of an encompassing cube, as illustrated below.
To obtain coordinates for the vertices of a dodecahedron, we have to work rather harder. First of all, we know from above that we can inscribe cubes inside a regular dodecahedron, so this suggests taking the coordinates ( We note that the green cube has edge length 2, and that PQ and QR are edges of a congruent cube. Hence PQ2 = (0 – ka)2 + (–a)2 + (ka – a)2 = 4, Also, P, Q and R form the vertices of a right angled triangle, so by Pythagoras’ theorem, PR2 = PQ2 + QR2, or a2+ (k + 1)2a2 + k2a2 = 2[k2a2 + a2 + (k – 1)2a2], Recall that Solving the above quadratic equation (**), we find that k = (3 + Substituting back in (*) gives a2 = 1/(1 + It follows that we can take as coordinates for the 20 vertices of the dodecahedron: ( The relationship between the numbers 20 (vertices) and 3 (coordinates) this time is
Here are some ideas.
Properties MathWorld : http://mathworld.wolfram.com/Dodecahedron.html Wikipedia : http://en.wikipedia.org/wiki/Dodecahedron Model making An older classic: Cundy, H. M., Rollett, A. P., Mathematical Models, Oxford (2nd Edition 1961) The excellent model book: Wenninger, M. J., Polyhedron Models, Cambridge (1971). Number of nets:
Inscribed polyhedra Animated cube in a dodecahedron : http://www.math.umn.edu/~roberts/java.dir/JGV/cube-in-dodeca.html | |||||||||||||||||||||||||||
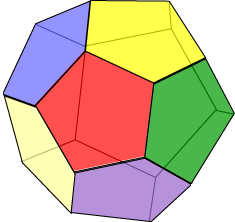
 , and faces? What does it tell us about this polyhedron?
, and faces? What does it tell us about this polyhedron? A net for the regular dodecahedron is given at right. It is known that for the dodecahedron (and for the icosahedron) there are 43380 distinct nets!
A net for the regular dodecahedron is given at right. It is known that for the dodecahedron (and for the icosahedron) there are 43380 distinct nets!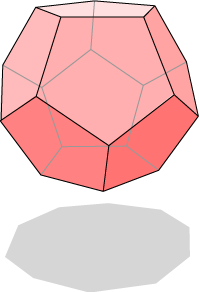 This first diagram shows one of the projections, where we obtain {10} as a shadow figure.
This first diagram shows one of the projections, where we obtain {10} as a shadow figure.