|
ICOSAHEDRON {3, 5}
For the record, here is a summary of some of the metric attributes of a regular icosahedron of side length s. Again, the values indicate some hard calculations!
The icosahedron has a number of interesting properties. We shall use our applet to investigate some of these.
The cross-sections make us work rather harder. Working from a model (if you have one) is probably easier than working from the applet.
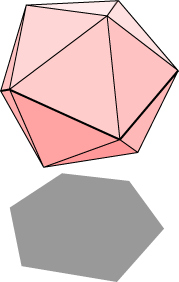
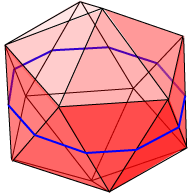
This left diagram below shows one of the projections, where we obtain {6} as a shadow figure. The view looks directly down through one of the triangular faces. The outline of the regular hexagon arises from a set of six linked edges of the icosahedron, three of which are shown in bold. The fact that these lie evenly between the top and bottom hexagonal faces shows that the resulting hexagonal projection is in fact regular. The figure at right shows the decagonal projection. We obtain this by looking down through one of the long diagonals of the icosahedron from one vertex to the opposite vertex. The shadow vertices are cast by the successive vertices of the antiprism forming the main body of the icosahedron.
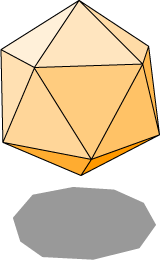
The triangular section {3} is given by any of the faces of the icosahedron. We will have to be satisfied with an ‘improper’ section. The figure below left shows a regular pentagonal section, occurring as the base of one of the pentagonal pyramid caps forming the icosahedron. At right is shown the regular decagonal section, with vertices at midpoints of edges of the equilateral triangles bounding the pentagonal antiprism.
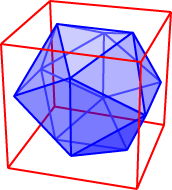
As we did with the dodecahedron, we now ask whether it is possible to inscribe a tetrahedron, a cube, or an octahedron nicely inside a dodecahedron.
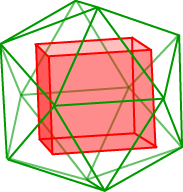
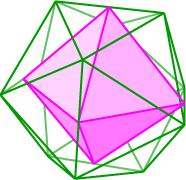
The diagrams below show that each of these inscribed polyhedra is possible. For the octahedron on the right, we observe that we can choose three parallel pairs of edges of the icosahedron which are mutually perpendicular. The midpoints of these six edges form the vertices of a regular inscribed octahedron. [Are the three pairs of edges parallel and mutually perpendicular? Consider one of the pentagonal pyramids forming the icosahedron, and let e denote one of the edges from the vertex. The plane of symmetry of the pyramid containing e passes through the altitude of the opposite triangular face, cutting the base f of that triangle perpendicularly. Thus edges e and f are perpendicular. Our result follows by applying this argument to each of the three pairs of edges in turn.] In the case of the cube, we choose as vertices eight triangular face centres of the icosahedron. But is the resulting figure a cube? Consider a triad of three adjoining triangular faces, with the centres of the outer two triangles located at the endpoints of a cube edge. By symmetry of the icosahedron, such triads will be congruent wherever they are placed on the icosahedron. It follows that the edge lengths of the ‘cube’ are all equal. Symmetry arguments also tell us that each ‘cube’ edge is parallel to the base of the central triangle of its triad. So the 12 ‘cube’ edges are parallel, in fours, to a set of three mutually perpendicular (and equal) edges of the icosahedron. Hence the ‘cube’ edges are not only equal but meet at right angles as required. To inscribe a regular tetrahedron, we simply use our known result about inscribing a tetrahedron in a cube.
You might like to think about the number of different ways each of these solids can be inscribed in an icosahedron. We defer consideration of inscribing a dodecahedron inside an icosahedron until later when we look at duality. However, there is an easy way to place the icosahedron inside a cube, using those three pairs of equal, parallel and mutually orthogonal edges of the icosahedron:
s2 = (
Finally, since each of these golden rectangles can be easily inscribed in a (diagonally placed) square, we find a nice way of placing an icosahedron inside an octahedron. Pick out the rectangles in the figure at right; notice how they are inscribed in the three determining squares of the octahedron. The vertices of the golden rectangles divide the edges of the octahedron in the golden ratio
From our above work with the three mutually orthogonal golden rectangles, we have obtained a nice symmetric set of vertex coordinates for the icosahedron:   , 1, 0),, 1),1, 0, ).
Here are some ideas.
Properties MathWorld : http://mathworld.wolfram.com/Icosahedron.html Wikipedia : http://en.wikipedia.org/wiki/Icosahedron Model making An older classic: Cundy, H. M., Rollett, A. P., Mathematical Models, Oxford (2nd Edition 1961). Number of nets:
Projections and sections Various: http://whistleralley.com/polyhedra/icosahedron.htm Inscribed polyhedra Animated cube in a dodecahedron : http://www.math.umn.edu/~roberts/java.dir/JGV/cube-in-dodeca.html Various: http://whistleralley.com/polyhedra/icosahedron.htm Golden rectangles The golden section: Coxeter, H.S.M., Introduction to geometry, Wiley (2nd Edition 1969), page 160.
In the projection, the edges of the projection arise from the zig-zag edges of the antiprism. Hence the midpoints of the zig-zag edges map to the midpoints of the edges of the regular decagon projection. Thus the decagon section is congruent to the regular decagon with vertices at the midpoints of the decagon projection.
|
Simple icosahedron properties
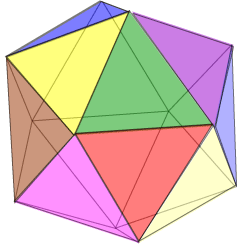
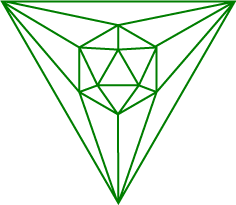At left is the Schlegel diagram for the icosahedron. Try counting the numbers of vertices, edges and faces. Are you satisfied this represents the icosahedron? Is it a planar graph? What is the importance of this?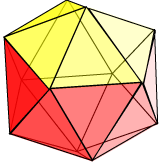
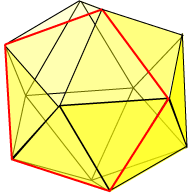
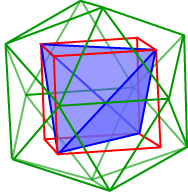
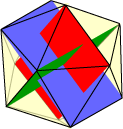With the dodecahedron and the icosahedron having so many regular pentagons associated with them, it shouldn’t surprise us to find some golden rectangles occurring. We can show that the rectangles having as opposite edges those three pairs of equal, parallel and mutually orthogonal edges of the icosahedron, are in fact golden rectangles. Furthermore, the rectangles themselves are mutually perpendicular.
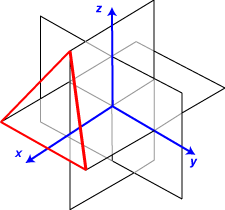Can we easily show that these rectangles are golden rectangles? It looks as though we might have to tackle the dreaded dihedral angles! Another idea is to work backwards, starting with three such golden rectangles of dimensions 
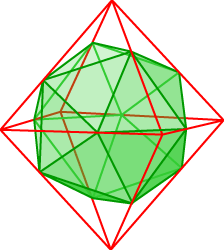Thus s = 2. The other distances are established similarly. Hence the vertices of the rectangle coincide with the vertices of a regular icosahedron.
4’, Discrete Mathematics 186 (1998) 69 – 94.