|
PLATONIC SOLIDS
The word ‘polyhedron’ (plural: polyhedra) comes from the Greek poly + hedron = many bases. We shall assume that the ‘bases’, or more commonly ‘faces’, are polygons.
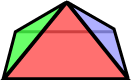
For example, at right is shown a square based pyramid. It is the region enclosed by five intersecting planes, each plane containing one of the faces. It has four triangular faces and one square face (base). It has eight edges and five vertices.
We now come to the Platonic solids or (equivalently) the regular polyhedra. Let us remind ourselves of our definition of a regular tessellation. A regular tessellation is a tessellation of congruent regular polygons in which each polygon shares a common edge with each of its neighbours. We noted here that •• the polygons have to be regular We now give the definition of a regular polyhedron. A regular polyhedron is a polyhedron such that •• the faces are regular Notice that the square based pyramid above may fail on all counts: the triangles need not be equilateral (regular), the faces are not all of the same type, and the vertices are not all alike: the face arrangement at the apex is different from that at the four base vertices.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
When we studied the regular tessellations, we considered m (
When we studied the regular tessellations, we considered m (
The five possible values of {n, m} for regular polyhedra are listed in the above table. No further rows or columns are necessary: six equilateral triangles or three regular hexagons would lead us to a planar tessellation. Notice that strictly, we haven’t established the existence of five regular polyhedra: there is no guarantee that the given polygon combinations will lead to a polyhedron that will ‘close’. However, in fact there are exactly five. These are illustrated below.
As we observed earlier, the Platonic solids were known to the ancient Greeks. They were described by Plato in his Timaeus ca. 350 BC. In this work, Plato equated the tetrahedron with the ‘element’ fire, the cube with earth, the icosahedron with water, the octahedron with air, and the dodecahedron with the quintessence (stuff!) of which the universe is made. One can’t help but wonder whether Plato would have preferred there to be just four regular polyhedra!
We defined above the terms vertex, edge and face of a polyhedron. We can easily count the number of each for the individual Platonic solids {n, m}, but you may be surprised to discover that we can actually calculate them from the values of n and m. Suppose our polyhedron has V vertices, E edges and F faces. First a reminder that Euler’s formula, defined for a planar map of V points, E edges and F regions is
A diagram of this type is called a Schlegel diagram, after the German mathematician Victor Schlegel (1843 – 1905) who discovered it. Consider now the regular polyhedron {n, m}.
V – E + F = 2, E = nF/2, and V = nF/m. Solving these equations (first substitute for E and V in Euler’s formula) gives:
Check some values of n and m to obtain values of F, V and E for the Platonic solids. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Coxeter, H. S. M., Introduction to Geometry, John Wiley (Edition 2) 1969, Chapter 10. |
 A convex polyhedron is a finite region of 3-dimensional space bounded by a finite number of planes. The part of each plane cut off by the other planes is a polygon called a face. Any common side of two faces is an edge of the polyhedron, and common vertex of three or more faces is a vertex of the polyhedron.
A convex polyhedron is a finite region of 3-dimensional space bounded by a finite number of planes. The part of each plane cut off by the other planes is a polygon called a face. Any common side of two faces is an edge of the polyhedron, and common vertex of three or more faces is a vertex of the polyhedron.


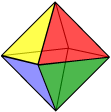
 The notation {n, m} for the regular polyhedra shows that the faces are regular {n}s and that there are m of them placed around each vertex. This notation, devised by Swiss mathematician Ludvig Schläfli (right) (1814 – 1895) is called the Schläfli symbol.
The notation {n, m} for the regular polyhedra shows that the faces are regular {n}s and that there are m of them placed around each vertex. This notation, devised by Swiss mathematician Ludvig Schläfli (right) (1814 – 1895) is called the Schläfli symbol.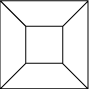 We take the cube as an example. Think of a skeletal cube, and place your eye close up against the centre of a square face. The cube will appear as at right: a planar graph. The numbers V and E remain unchanged. The exterior region of the graph is of no interest to us, but if in our counting for F we replace this region by the face we are looking through; the number F of faces equals the number F of regions. Hence Euler’s formula holds for the cube. A similar argument holds for each convex polyhedron.
We take the cube as an example. Think of a skeletal cube, and place your eye close up against the centre of a square face. The cube will appear as at right: a planar graph. The numbers V and E remain unchanged. The exterior region of the graph is of no interest to us, but if in our counting for F we replace this region by the face we are looking through; the number F of faces equals the number F of regions. Hence Euler’s formula holds for the cube. A similar argument holds for each convex polyhedron.