|
SQUARE {4} The
A square has four equal sides, and four equal angles each measuring 90°. It has two diagonals which bisect each other at right angles. Another way of saying this, is to say that a square is a special quadrilateral (four sided polygon) which is both equilateral and equiangular. It is the intersection of the family of (equiangular) rectangles which have equal diagonals, and the family of (equilateral) rhombuses which have perpendicular diagonals.
We shall describe the symmetries of the square, and this will set the pattern for the remaining regular polygons.
This group of eight distance preserving transformations is called the dihedral group, D4. In general, the symmetries of the regular n-gon form the dihedral group of degree n, Dn, containing 2n symmetries – n rotations (including the identity), and n reflections. You might notice that for the equilateral triangle we used the term symmetric group, S3. In fact, this coincides with D3, but for n = 3 the symmetries permute the vertices in all possible 3! ways; that is, we get all possible symmetries (of the points). This only happens for n = 3.
As for the equilateral triangle, there are some interesting mathematical results in which the square unexpectedly appears.
Click to confirm your answer. Of course it is a square! A more satisfying result, also an obvious analogue of Napoleon’s Theorem, is the following.
Click to confirm your answer. This is obviously an analogue to the Napoleon Theorem for triangles. The result holds true if the squares are constructed inwards on the sides of the parallelogram. If the squares are constructed on the sides of a general quadrilateral, the centres no longer form the vertices of a square, but a partial result still remains true. What is it? This is known as van Aubel’s Theorem. You might like to think of further ways in which these results might be generalized.
The title may make us think of chess, but there are other games and puzzles which rely on the square for their structure. The first of these are the well known magic squares.
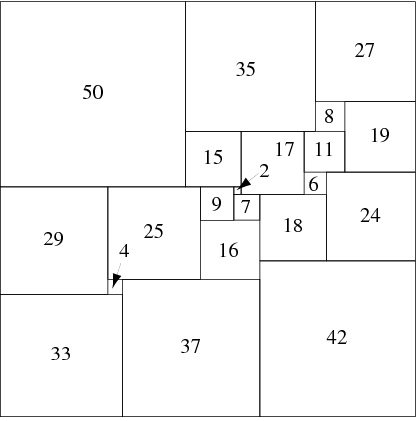
Now check your answers. Another topic which may be classed as recreational is the topic of square dissections. It is obviously possible to subdivide a given square into smaller equal squares. But can we dissect a given square into a finite number of unequal squares? In 1978, Duijvestijn discovered a dissection into 21 smaller squares. It is known that this is the smallest possible number.
Duijvestijn’s dissection of a square into 21 smaller squares.
The theory of groups : http://internal.maths.adelaide.edu.au/people/pscott/groups/gpf/ Finsler and Hadwiger result : Finsler, P. and Hadwiger, H., Einige Relationen im Dreieck, Commentarii Mathematici Helvetici 10 (1937) 316 – 326. van Aubel’s Theorem : van Aubel, H. H., Note concernant les centres de carrés construits sur les côtés d'un polygon quelconque, Nouvelle Correspond. Math. 4 (1978) 40 – 44. Magic Squares : http://mathforum.org/alejandre/magic.square.html Square Dissections : Duijvestijn, A. J. W., A Simple Perfect Square of Lowest Order, Journal of Combinatorial Theory (Series B) 25, (1978) 240 – 243.
|
second convex regular polygon in our sequence is the square {4}. 
Intrinsic Properties 
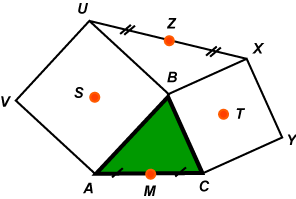First a result due to Finsbury and Hadwiger which is a little reminiscent of the Napoleon Theorem for triangles.
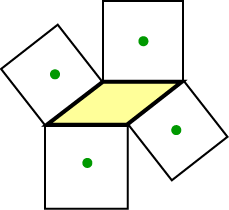side. Consider the centres of these four squares. Can you make a conjecture? What previous result does this remind you of?
