SNUB CUBE
32{3} + 6{4}, 3.3.3.3.4 or 3⁴.4

  Definition and notation

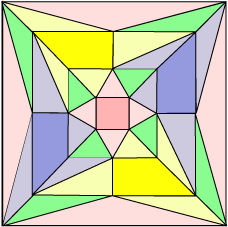
The snub cube can be constructed in the following way. Starting with a cube, the faces are pulled outwards, all given a small clockwise turn, and adjusted in their placing so that the remaining surface is filled exactly with equilateral triangles. The solid has a definite orientation. A snub cube of reverse orientation can be constructed as above, by giving all the cube faces an anti-clockwise turn. The solid can be nicely coloured to illustrate this construction. Here the dark red, yellow and blue squares are derived from the original cube. Each square face is surrounded by its won ring of four equilateral triangles, and green equilateral triangles are placed at regular intervals to fill in the remaining gaps.

The snub cube can also de derived from the octahedron, and is sometimes called a snub octahedron or a snub cuboctahedron, combining the two properties. We look more closely at this shortly.

• How many faces, edges, vertices does it have?
   Complete the table below (# stands for ‘number of’).

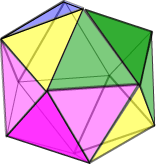
Defect angle	V	# triangular faces	# square faces	F	E	V – E + F

• Draw a Schlegel diagram for this solid.

Check your answers ...

   You should have obtained:

This Schlegel diagram is interesting in that it demonstrates that the solid has an orientation.

You might like to count the triangles and the ‘squares’, and check out the way that they are arranged.

MathWorld gives some details about various measurements associated with this solid.

  Further properties

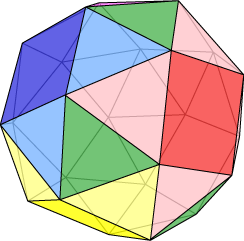
As before, we can use this Java applet to play with each of the Archimedean solids. Take time to enjoy the different views. Look for special symmetries and nice arrangements of faces and edges.

• Can you place this polyhedron so that you see
     –  one square face + 16 triangular faces
     –  two square faces + 16 triangular faces
     –  two square faces + 14 triangular faces?
What other combinations can you find?

• Notice the lovely red bands that surround the green ‘interior’.  

  Model making

The making of the model of the snub cube is an interesting challenge, but not difficult. See this link for some details.

  The snub family

From the first paragraph above we quote:

(In the construction of the snub cube) ... the dark red, yellow and blue squares are derived from the original cube. Each square face is surrounded by its won ring of four equilateral triangles, and green equilateral triangles are placed at regular intervals to fill in the remaining gaps.

If we imagine the arrangement of the cube and the octahedron in forming a cuboctahedron, we see that the eight green triangles correspond to the eight faces of the octahedron, pulled apart and twisted. Each such face is then surrounded by three triangles, and the remaining spaces filled with squares.

This suggests that there might be other polyhedra which can be constructed in this way.

• Starting with a regular tetrahedron, see if you can use the above process to form a ‘snub tetrahedron’. It is a polyhedron we have already seen. Which one?

Check you answer ...

You might expect there to be a further member of the snub family. Why? We shall come to it later!

  Vertex coordinates

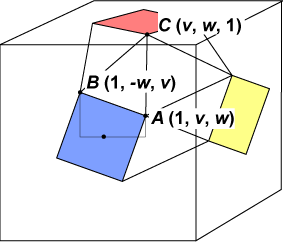
Let us take the original cube to have vertices (1, 1, 1). This means that the face planes are x = 1, y = 1 , and z = 1. Suppose the snub cube has edges of length l, and let A, B, C be vertices as shown in the figure. We take the ‘blue’ face, the ‘yellow’ face and the ‘red’ face to by x = 1, y = 1 and z = 1 respectively. The construction has an obvious rotational symmetry, so assuming A has coordinates (1, v, w) (with 1 > v > w > 0), we easily obtain B (1, – w, v) and C (v, w, 1).

The drawn segments are all edges of the snub cube, so all have length l, which we can now calculate.

We obtain

             AB²  =  l²  =  (v + w)² + (w – v)²  =  2(v² + w² ) ,
and
            AC²  =  l²  =  (1 – v)² + (v – w)² + (w – 1)²  =  2(v² + w² – vw – v – w + 1) ,
and
            BC²  = l²   = (1 – v)² + 4w² + (v – 1)²  =  2(v² + w² + w² – 2v + 1).

Subtracting, we get

                       vw + v + w – 1  =  0 ; that is     v(1 + w)  =  (1 – w),
and
                      vw + w² + w – v  =  0 ; that is    v(1 – w)  =  w(1 + w) .

Multiplying these two equations together, we obtain

                     v² (1 – w² ) = w(1 – w² ), and since  w² <  1 we deduce that   v² = w.

Furthermore,

                    vw + v + w – 1 = 0   and   l² = 2(v² + w² ) give

                                v³ + v² + v – 1 = 0 , and l² = 2(v⁴ + v² ) .

We see that the vertex coordinates of A are (1, v, v²), where v is the real solution of v³ + v² + v = 1. This is found, numerically or otherwise, to be approximately 0.54369. Using the rather constrained symmetry of the snub cube, the vertex coordinates are found to be:

                all even permutations of  (1, v, v²) having an even number of + signs

and

               all odd permutations of  (1, v, v²) having an odd number of + signs.

There are 12 of each of these, (three permutations, and four sign arrangements) giving a total of 24 coordinate sets, as expected. In the first case, remember the sign combination    – – – .

References

It is the icosahedron. Notice the dark coloured faces surrounded by triangles, and further equilateral triangles filling the gaps.