| |
 SNUB SNUB
DODECAHEDRON
80{3} + 12{5}, 3.3.3.3.5 or 34.5
 Definition and notation Definition and notation
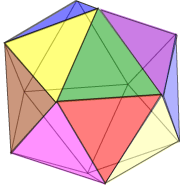
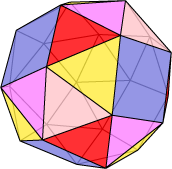
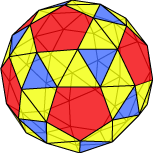
This is the last of our Archimedean solids. It belongs to the ‘snub’ family we looked at earlier. You can think of taking a regular dodecahedron, and pulling the faces apart, outwards from the centre. Each face is the rotated a little, for example in a clockwise direction, and placed so that the spaces in between can be filled with equilateral triangles. You might see the structure better with this colouring. If the faces are rotated in the opposite direction we obtain a snub dodecahedron with opposite orientation. The blue triangles correspond to the icosahedron which is dual to the original dodecahedron. For this reason, this solid is sometimes called the snub icosahedron or the snub icosidodecahedron.
• How many faces, edges, vertices does the rhombitruncated icosidodecahedron have?
Complete the table below (# stands for ‘number of’).
• Draw a Schlegel diagram for this solid. (This requires dedication! I started from a central pentagon and worked outwards.)
Check your answers ...
 You should have obtained: You should have obtained:
| Defect angle |
V |
# triangular faces |
# pentagonal faces |
F |
E |
V – E + F |
| 12° |
60 |
80 |
12 |
92 |
150 |
2 |
The defect angle is 360° – (4 x 60)° – 108° = 12°. From our previous work, V = 720 /12 = 60. The number of faces is given under the title as 80 + 12. The number of edges can now be derived from Euler’s formula, or as usual, we can compute the number of edges by 3 x 80 + 5 x 12 = 300, and divide this number by two, since each edge is counted twice. An example of a Schlegel diagram for the snub dodecahedron is:
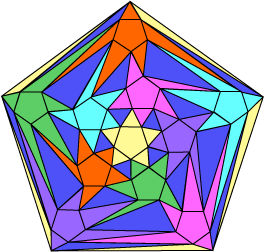
You might like to count the various faces by type, and check out the way that they are arranged. Notice that this figure has a definite orientation.
MathWorld gives some details about various measurements associated with this solid.
 Further properties Further properties
As before, we can use this Java applet to play with each of the Archimedean solids. Take time to enjoy the different views. Look for special symmetries and nice arrangements of faces and edges.
• Make a list of the numbers of visible blue pentagons and red triangles that can be seen at any one time.
• Notice the lovely red bands that surround the blue ‘interior’.
 Model making Model making
The making of the model of the snub dodecahedron involves a large number of faces. See this link for some details.
 The snub family The snub family
The snub dodecahedron is the final member of the subset of the Archimedean solids we have called the snub family. You may recall that we have already looked at the snub cube (octahedron, cuboctahedron), and the rather more trivial snub tetrahedron. The three solids in this family are all constructed in the same way, by pulling the faces of the original solid out from the centre, twisting them a little in the same direction, and then filling the spaces with equilateral triangles. They are pictured below, together with the original regular polyhedra.
|
|
|
|
|
Tetrahedron
Snub tetrahedron
|
Cube
Snub cube
|
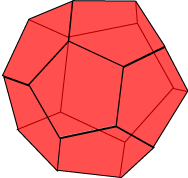
Dodecahedron
Snub dodecahedron
|
|
|
|
|
 Vertex coordinates Vertex coordinates
You can find a list of the Cartesian coordinates (without proof) for the vertices of a snub dodecahedron in Wikipedia.
These are all the even permutations of
(±2 , ±2, ±2 , ±2, ±2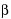 ), ),
(±(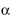 + + 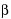 / / + +  ), ±(- ), ±(-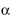  + + 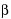 + 1/ + 1/ ), ±( ), ±(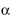 / / + +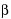  – 1)), – 1)),
(±(–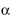 / / + + 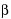  + 1), ±(– + 1), ±(–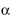 + + 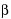 / / – –  ), ±( ), ±(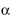  + + 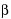 – 1/ – 1/ )), )),
(±(–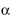 / / + + 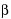  – 1), ±( – 1), ±(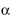 – – 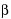 / / – –  ), ±( ), ±(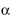  + + 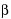 + 1/ + 1/ )) and )) and
(±(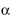 + + 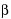 / / – –  ), ±( ), ±(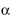  – – 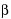 + 1/ + 1/ ), ±( ), ±(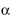 / / + + 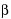  + 1)), + 1)),
with an even number of plus signs, where
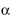 = x – 1/x = x – 1/x
and
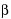 = x = x + + 2+ 2+ /x, /x,
where  = (1+ = (1+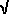 5)/2 is the golden mean and x is the real solution to x3 – 2x = 5)/2 is the golden mean and x is the real solution to x3 – 2x = , which is approximately 1.7155615. Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph (solid with the opposite orientation) of the other one. , which is approximately 1.7155615. Taking the odd permutations of the above coordinates with an odd number of plus signs gives another form, the enantiomorph (solid with the opposite orientation) of the other one.
The reference for vertex coordinates below contains a rather difficult proof establishing a set of vertex coordinates.
 References References
MathWorld : http://mathworld.wolfram.com/SnubDodecahedron.html
Wikipedia : http://en.wikipedia.org/wiki/Snub_dodecahedron
 Construction : Wenninger, M. J., Polyhedron models, Cambridge (1971). Construction : Wenninger, M. J., Polyhedron models, Cambridge (1971).
Cundy, H. M., Rollett, A. P., Mathematical models, Oxford (1961).
Vertex coordinates:
www.emis.de/journals/BAG/vol.43/no.1/b43h1wem.pdf
Weissbach B., Martini, H., On the chiral Archimedean solids, Beiträge zur Algebra und Geometrie Vol 43 (2002) No 1, 121 – 133.
|
 SNUB
SNUB