|
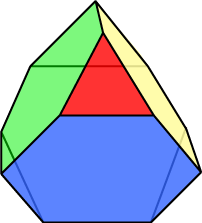
4{3} + 4{6}, or 3.6.6 Our first Archimedean or semiregular polyhedron is the truncated tetrahedron, illustrated at right.
The notation 4{3} + 4{6} tells us that this solid has four equilateral triangles and four regular hexagons as faces. The 3.6.6 notation gives the arrangement of faces about each vertex. The defect angle is 360° – 120° – 120° – 60° = 60°. From our previous work, V = 720 / 60 = 12. Of course, it is easy to count them directly here. We might decide to determine the number of edges from Euler’s formula, V – E + F = 2, which would be fine, if we could be sure that Euler’s formula held for this solid. One way of doing this would be to draw a Schlegel diagram for the polyhedron: a planar representation having no lines crossing. Remember we can do this by ‘looking closely through a face’. For example, we might get here: You can see the four red triangular faces. The three blue hexagonal faces (like three of the red triangles) are not to scale; the fourth hexagonal face is the outer boundary: the face being looked through.
Like this ... original tetrahedron ... doing the truncation ... the final truncated tetrahedron. MathWorld gives some details about various measurements associated with this solid.
As with the Platonic solids, we can use this Java applet to play with each of the Archimedean solids. Perhaps you can find some interesting new property! It is not impossible: new results are being discovered in elementary geometry even today. The only reason they have not been discovered before is that no-one thought to ask the right question.
The model of the truncated tetrahedron is easy to make. See this link for some details.
The remaining vertices are then the 12 trisection points of the tetrahedral edges:
Wikipedia : http://en.wikipedia.org/wiki/Truncated_tetrahedron MathWorld : http://mathworld.wolfram.com/TruncatedTetrahedron.html University of Manitoba : http://home.cc.umanitoba.ca/~gunderso/pages/archimedean_solids/truncated_tetrahedron.htm Construction : Wenninger, M. J., Polyhedron models, Cambridge (1971).
It looks as though the total angle defect is always 720° = 4
In fact this is not quite correct, as we shall see below. |
 TRUNCATED TETRAHEDRON,
TRUNCATED TETRAHEDRON, 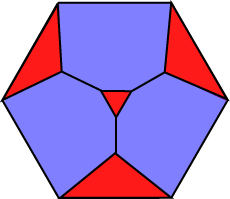
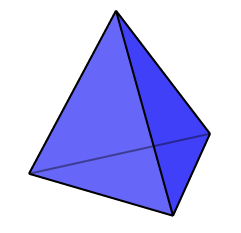 The name truncated tetrahedron arises because this solid is obtained by carefully cutting off (or truncating) the vertices of a regular tetrahedron. We start with a regular tetrahedron, and divide each edge equally into three parts. Joining these trisection points gives rise to the equilateral triangle and regular hexagonal faces of the truncated tetrahedron.
The name truncated tetrahedron arises because this solid is obtained by carefully cutting off (or truncating) the vertices of a regular tetrahedron. We start with a regular tetrahedron, and divide each edge equally into three parts. Joining these trisection points gives rise to the equilateral triangle and regular hexagonal faces of the truncated tetrahedron.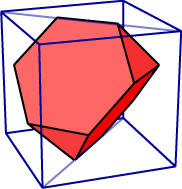 We already have some nice vertex coordinates for a tetrahedron derived from a cube. Since we wish to trisect the edges of the tetrahedron to create this polyhedron, this suggests we take the tetrahedral vertices to be
We already have some nice vertex coordinates for a tetrahedron derived from a cube. Since we wish to trisect the edges of the tetrahedron to create this polyhedron, this suggests we take the tetrahedral vertices to be