59 STELLATIONS OF
THE ICOSAHEDRON :

THREE NEW POLYHEDRA

Fifty-nine is a lot of stellations! Or even 58, if you choose not to count the initial icosahedron. As this site is aiming to just give an introduction to the polyhedra, we give here three examples of the stellations. If you wish to investigate further, you are referred to the references at the end of this page.

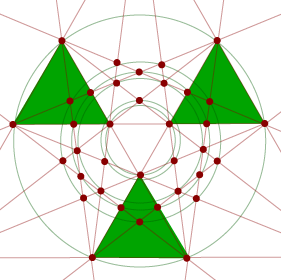
  The triakis icosahedron

This is the first stellation of the icosahedron. For each triangular face, you can imagine the three adjoining faces extended up to form a shallow triangular pyramid rising above that face. The rather strange ‘triakis’ descriptor obviously has tri (= 3) as its root, and refers to the adding of three new triangular faces to each face of the icosahedron.

•   Check stellation #1 in the above applet. Play with the applet to get a feel about how this stellation is constructed.

•   In the adjacent figure, check out the central  icosahedron.

In the applet this stellation is designated #1. You may find is designated #2 in other lists, with the original icosahedron listed as #1. In fact there is no unique listing of the stellations, as different criteria can be used to establish the ordering.

The stellation diagram for this polyhedron is given by:

The numbers of vertices, edges and faces of this polyhedron and of the underlying icosahedron are given below.

 
   V   
   E   
   F   
V – E + F
Triakis icosahedron
32
90
60
2
Icosahedron
12
30
20
2

We see that Euler’s Formula continues to hold here.

•  Using the applet, or the picture of this solid, see if you can relate the values of V, E, F  for the triakis icosahedron to those of the icosahedron.



Looking first at the vertices, we observe that each vertex of the original icosahedron occurs as a vertex of the triakis icosahedron, and the tetrahedral caps provide 20 more. So we have 12 + 20 = 32. For the edges, each face has the 3 original edges plus 6 more – the outline of the green triangles in the stellation diagram. Since each edge occurs twice, this gives (3 + 6) x 20 / 2 = 90. For each original icosahedral face, we have 3 faces of the triakis icosahedron, giving 3 x 20 = 60.


It is easy to construct a model for this stellation.




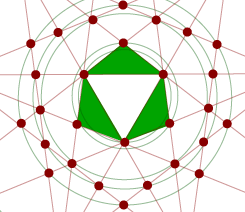
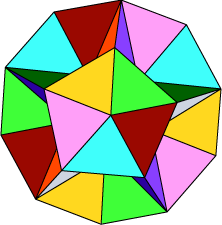  Stellation #25 – a deltahedron

Our next polyhedron has some interest, because although it is a stellation of the icosahedron, its structure appears to be based on the dodecahedron.

• Use the applet to check that this is indeed stellation #25.
    In the diagram at right, the triangles of the same colour lie in a plane. Use the applet to determine how this arrangement relates to the original icosahedron.
   Play with the applet to get a feel of this pretty solid.


This polyhedron belongs to a general family of polyhedra known as deltahedra. The Greek capital D is Delta ( 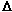), and the deltahedra are simply those polyhedra for which every face is an equilateral triangle. The family includes the regular tetrahedron, octahedron and icosahedron. In the present case, it is clear that although the faces are all congruent equilateral triangles, the vertices are not all alike.

The stellation diagram for this polyhedron is given below. The central triangle is the icosahedral face.


The numbers of vertices, edges and faces of this polyhedron and of the underlying icosahedron are given below.

 
   V   
   E   
   F   
V – E + F
Stellation #25
32
90
60
2
Dodecahedron
20
30
12
2

We see that Euler’s Formula continues to hold here.

•  Using the applet, or the picture of this solid, see if you can relate the values of V, E, F  for this deltahedron to those of the dodecahedron. (You might observe that the values of V, E and F for Stellation #25 are the same as for the triakis icosahedron.)



Let’s start with the faces. We have a 12 faced dodecahedron with pentagonal dimples. This gives a count of 12 x 5 = 60 faces. Alternatively, from the stellation diagram, each of the 20 faces of the icosahedron gives rise to 3 new faces for the stellation, again giving 20 x 3 = 60. For the vertices, there are the 20 vertices of the dodecahedron plus the 12 inner vertices of the dimples giving 20 + 12 = 32. Finally, the dodecahedron has 30 edges, and each of the 12 dimples contributes a further 5, giving a total of 30 + (12 x 5) = 90.


You might like to make the attractive model of this stellation. You might notice that you can use this construction to make a different deltahedron (not a stellation of the icosahedron) by assembling the dimples so that they face outwards.




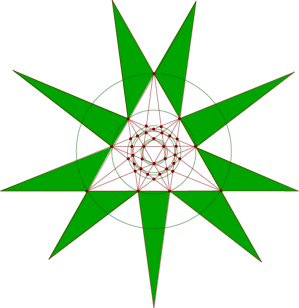
  Spiky stellation #7

In some classifications, this spiky star is called the final stellation of the icosahedron.

• Use the applet to check that this is indeed stellation #7.
   Play with the applet to get a feel of this pretty solid.
   Notice the intersecting star polygons (each with a single colour).



This complicated model has 60 trihedral spikes, occurring in clusters of five. Each cluster has a regular pentagon as its base, and the 12 clusters fit together about a regular dodecahedron.


The stellation diagram for this polyhedron is given below. The central triangle is the icosahedral face. Each face contains the (green) 9-vertex star polygon.

The numbers of vertices, edges and faces of this polyhedron and of the underlying icosahedron are given below.

 
   V   
   E   
   F   
V – E + F
Stellation #7
 92
270 
 180
2
Dodecahedron
20
30
12
2

We see that Euler’s Formula continues to hold here.

•  Using the applet, or the picture of this solid, see if you can relate the values of V, E, F  for this stellation to those of the dodecahedron.


Let us try to verify these results geometrically. First of all, the number V of vertices. There are 60 star points, plus the 20 vertices of the inner dodecahedron, plus 12 face centres where the components of each cluster of spikes meet on the inner dodecahedron. Thus V = 60 + 20 + 12 = 92.
For the faces, we have 3 x 60 = 180, counting the faces of the 60 trihedral spikes.
Then there are the edges. Here we have first of all 3 x 60 edges of the spikes. To this we add the 30 edges of the inner dodecahedron – formed by the outer edges of each spike cluster. There are also a further 5 edges on each dodecahedral face, radiating from the centre to the face vertices, corresponding to where the spikes join together. Thus the total number of edges is E = 180 + 30 + (5 x 12) = 270. As a final check we note that these values satisfy Euler’s Formula.

This stellation gives rise to a very attractive model. Because of the extremely complicated nature of this model, I would suggest you use the net given in the Tarquin book below. I found that this gives a very satisfying model with little pain!





  References

Coxeter, H. S. M., du Val, P., Flather, H.T., and Petrie, J. F., The 59 icosahedra, University of Toronto (1951).
                                [The classic reference on this topic.]
A newer version of this book can be accessed through Amazon on
http://www.amazon.com/gp/product/1899618325/ref=nosim/002-2157352-7234419?redirect=true&n=283155

Coxeter, H. S. M., Regular Polytopes, Macmillan 2nd Ed. (1963).

Jenkins, G., The Final Stellation of the Icosahedron (Tarquin Polyhedra) (Paperback) (1965).

Math Consult : http://www.mathconsult.ch/showroom/icosahedra/index.html

Wenninger, M. J., Polyhedron Models, Cambridge (1979).
                              [Note that Wenninger’s numbering differs from that given here.]

Wolfram MathWorld : http://mathworld.wolfram.com/IcosahedronStellations.html