|
Our main interest is in tessellations which involve the regular polygons, but there are several other types of tessellation which either commonly occur, or which have great intrinsic interest. We look at these briefly.
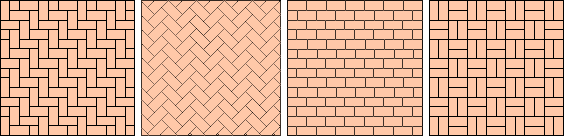
A common paving brick forms a 2 x 1 rectangle.
|
||||||||
|
Our main interest is in tessellations which involve the regular polygons, but there are several other types of tessellation which either commonly occur, or which have great intrinsic interest. We look at these briefly.
A common paving brick forms a 2 x 1 rectangle. Several types of common brick paving patterns are shown below. Of course, as a tessellation, there is no difference between the first two, but the angle of the second gives the paving a different appearance.
Since each of these tessellations only involves one basic shape, they can’t be classed as semiregular, but they also fail to be regular as the rectangle is not a regular polygon. Notice too that in each case, each brick has at least two vertices at the midpoints of neighbouring edges – a behaviour disallowed in our previous definitions. |
||||||||
|
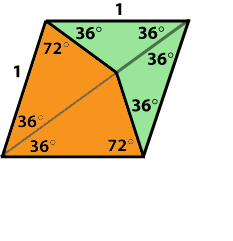
We know that the ratio of the diagonal of a regular pentagon to the side length is 1 : It is clear that the kite and dart can be used to form a periodic tessellation: we simply tessellate the given rhombus in the obvious way. But the kite and dart fit together in other more interesting ways. For example:
Here are some properties of the Penrose tilings. •• Every finite portion of any tiling is contained infinitely often in every other tiling It is fun to explore these tilings on your own. You can buy a commercial set of tiles, or print off several copies of this linked page onto light card, cut out the tiles, and then play! |
||||||||
|
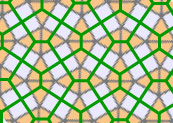
This is a tessellation which appears in the streets of Cairo, and in Islamic art. We can think of the tessellation as being made up of two overlapping tessellations of congruent hexagons, intersecting each other at right angles.
In fact, the remaining angles are not completely determined. We would like our pentagons to retain an axis of symmetry, meaning the two base angles should be equal, and the three non-right angles must add to 360°, but other than that, they can vary. Here is a variation with the non-right angles each 120°.
The Cairo tessellation occurs as a projection of the regular dodecahedron (later) and as the dual of the semiregular tessellation of squares and equilateral triangles, 3.3.4.3.4.
Brick paving patterns
This advertisement show some of the possibilities : http://www.pburch.net/toys/B1915068958/C522364530/E1218854721/ A wonderful gallery of Penrose tilings : http://www.josleys.com/creatures34.htm
|
||||||||

 In 1974, while Roger Penrose was a graduate student at Cambridge, he became interested in non-periodic tilings. By non-periodic we mean that there is no translation which maps the tiling onto itself. Penrose found a wonderful tiling of this type which only involves two tiles: a kite and a dart.
In 1974, while Roger Penrose was a graduate student at Cambridge, he became interested in non-periodic tilings. By non-periodic we mean that there is no translation which maps the tiling onto itself. Penrose found a wonderful tiling of this type which only involves two tiles: a kite and a dart.