SEMIREGULAR TESSELLATIONS

  Definition and notation

We can extend the idea of a regular tessellation to the case where more than one regular polygon is used. In this case we have also to add a condition about the polygons circling each vertex. Example of semiregular tessellations are shown at right.

A semiregular tessellation of the plane is a tessellation involving more than one type of regular polygon, in which the same arrangement of polygons occurs about every vertex.

The semiregular tessellations are often denoted by a sequence of numbers corresponding to the polygons arranged about a vertex. So the top figure at right would be denoted 4.8.8 (square, octagon, octagon), and the figure below by 3.4.6.4. When using the term ‘same arrangement’ we allow clockwise or anticlockwise orientation about the vertex.


  Can we list the semiregular tessellations?

There are a number of obvious questions now. How many semiregular tessellations are there? What do they look like? How can we find them? How can we be sure we have all of them?

Notice that as before, we require at least three polygons at each vertex. Also, since the equilateral triangle has the smallest vertex angle amongst the regular polygons, there can be at most six polygons meeting at a vertex.

We need a strategic approach. Here is an idea.

1. Tessellations with three polygons at a vertex
     (a) Triangles, squares, ...
     (b) Squares, pentagons, ...
     (c) Pentagons, hexagons, ...
     (d) Hexagons (We can ignore this case: three hexagons at a vertex determine the regular hexagonal tessellation.)

2. Tessellations with four polygons at a vertex
     (a) Triangles, squares, ...
     (b) Squares  (We can ignore this case: four squares at a vertex determine the regular square tessellation.)

3. Tessellations with five polygons at a vertex
     (a) Triangles, squares, ...

4. Tessellations with six polygons at a vertex
     (We can ignore this case: six triangles at a vertex determine the regular triangular tessellation.)

A simple way of exploring this is to write a simple computer program Here is a Pascal program that deals with Case 1 above. If three polygons {a}, {b} and {c} meet at a vertex, then the sum of the interior angles must add to 2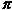. That is, (cancelling the ):

a – 2  +  b – 2  +  c – 2
a             b            c   
  =   2.

  

Here is the program:

program semiregular1;

var
a, b, c: Integer;
N : real;

begin {program}

for a:= 3 to 50 do
for b:= 3 to 50 do
for c:= 3 to 50 do
begin{for}
N:= (a-2)/a + (b-2)/b + (c-2)/c;
if (a <= b) and (b <= c) and (N = 2) then
writeln(a, b, c);
end{for};
end.

The number 50 in this program is rather arbitrary, but we shall see that the exact (largish) value is not important.

•  (a) If you are into computing, compile and run the above program, or rewrite it in the language of your choice. List the results.
    (b) Next, adapt the program to cover the cases where four or five polygons meet at a vertex. List the results.


You should have obtained the following possibilities. Notice that there may well be fewer semiregular tessellations than the 21 cases listed here. On the other hand, in some cases the given polygons can be arranged in two different ways around the vertex. We have listed these in brackets.

3.7.42, 3.8.24, 3.9.18,  3.10.15,  3.12.12,
4.5.20,  4.6.12,  4.8.8,
5.5.10


3.3.4.12,  (3.4.3.12), 3.3.6.6,  (3.6.3.6), 3.4.4.6,  (3.4.6.4)


3.3.3.3.6,  3.3.3.4.4, (3.3.4.3.4)

We now show that only the eight green sets correspond to semiregular tessellations. Thus far we have only looked at the polygon behaviours about a single vertex. But this behaviour has to be repeated at every vertex.


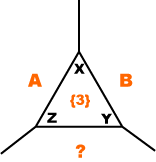•  (a) In the figure at right, suppose that we are looking at part of a semiregular tessellation 3.A.B where A and B are different numbers. First look at vertex Y. What must you substitute for the question mark? Now look at vertex Z. What must the question mark be now? Do you have a problem? What do you conclude?
    (b) Consider the same situation, only where the triangle is replaced by a regular pentagon. Do you have the same problem?
    (c) Now investigate the case where we have three polygons meeting at a vertex, and the triangle is replaced by a square. Do you get two possibilities here? What are they?

We observe that the question mark has to be replaced by A to make vertex Y fit the pattern, and by B to make vertex Z right. This contradiction can be righted only by assuming that polygons {A} and {B} are congruent. Thus we must have 3.A.A, leading to 3.12.12 being the only possibility of this type. Similarly 4.5.20 and 5.5.10 are easily excluded.

In the case of the square, we finish up with just two possibilities: 4.A.B and 4.A.A. Our computer program and the above reasoning now shows that 4.6.12 and 4.8.8 are the only possibilities of this type.

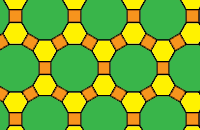
You can now apply an exactly similar argument to eliminate 3.3.4.12,  3.4.3.12, 3.3.6.6,  and 3.4.4.6. We are now left with eight possibilities – the green combinations. None of this guarantees that these will form semiregular tessellations: there may be some other constraint we haven’t investigated yet! But in fact we obtain precisely eight as shown below.
3.3.3.3.6 3.3.3.4.4 3.3.4.3.4 3.4.6.4
3.6.3.6 3.12.12 4.6.12 4.8.8

  Some practical work

One gets a better feel of the tessellations by actually constructing them. The linked page contains the types of polygons used to the semiregular tessellations. Print off four copies of the page on sheets of thin card; you can vary the size of your copy to suit. Then cut out the various polygons. Experiment with placing the polygons in different positions to verify the above theory.


Duality

There is some interest in investigating the duals of the semiregular tessellations. However, whereas the duals of the regular tessellations are again regular, the duals of the semiregular tessellations are not themselves semiregular. For example, 4.4.8 gives rise to a tesselation of right-angled isosceles triangles.


Real life occurrences

It is harder to find occurrences of the semiregular tessellations in real life. The 4.4.8 tessellation is the most common, occurring in pavings, tilings and Japanese woodcraft. The first website below gives some further examples from Islanic art and old ornamentation.