| |
TRUNCATED OCTAHEDRON
6{4} + 8{6}, 4.6.6
  Definition and notation Definition and notation
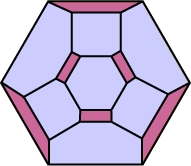
Our next Archimedean or semiregular polyhedron is the truncated octaahedron, illustrated at right.
You may prefer the two-colour version.
• How many faces, edges, vertices does it have?
Complete the table below (# stands for ‘number of’).
• See if you can construct a Schlegel diagram for this solid. Don’t be satisfied with ‘any old effort’. Find a classy figure!
Check your answers ...

 You should have obtained: You should have obtained:
| Defect angle |
V |
# square faces |
# hexagonal faces |
F |
E |
V – E + F |
| 30° |
24 |
6 |
8 |
14 |
36 |
2 |
The defect angle is 360° – 120° – 120° – 90° = 30°. From our previous work, V = 720 / 30 = 24. We could also count them directly here.
Here is a pretty classy Schlegel diagram! Check that it has the right numbers of ‘squares’ and hexagons.
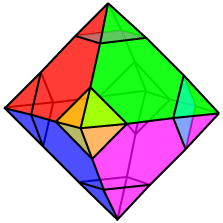
 Of course we obtain the truncated octahedron by carefully cutting off (or truncating) the vertices of a regular octahedron. We start with a regular octahedron, and simply trisect each edge into three equal parts. Joining these trisection points gives rise to the squares and regular hexagonal faces of the truncated octahedron. Notice that it is the requirement for regular hexagons that controls the choice of points here. Of course we obtain the truncated octahedron by carefully cutting off (or truncating) the vertices of a regular octahedron. We start with a regular octahedron, and simply trisect each edge into three equal parts. Joining these trisection points gives rise to the squares and regular hexagonal faces of the truncated octahedron. Notice that it is the requirement for regular hexagons that controls the choice of points here.
Here is how it works ... original octahedron ... doing the truncation ... the final truncated octahedron.
MathWorld gives some details about various measurements associated with this solid.
 Further properties Further properties
As previously, we can use this Java applet to play with each of the truncated octahedron. Enjoy this pretty solid!
• Place the solid so that the outline is
– an irregular hexagon
– an irregular octagon
– an irregular dodecagon.
• Place the solid so that the projection is made up of
– a square + four congruent hexagons
– four hexagons and three congruent rectangles
– two congruent rhombi + two congruent hexagons
– three hexagons + three rectangles + two congruent rhombi.
 Model making Model making
The model of the truncated tetrahedron is easy to make. See this link for some details.
  Vertex coordinates Vertex coordinates
If we take the original octahedron to have vertices
then be taking the trisection points of the edges we obtain the 24 vertices
(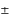 2, 2, 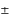 1, 0), ( 1, 0), (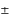 1, 1, 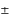 2, 0), ( 2, 0), (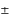 2, 0, 2, 0, 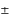 1), ( 1), (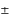 1, 0, 1, 0, 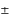 2), (0, 2), (0, 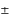 1, 1, 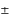 2), (0, 2), (0, 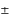 2, 2, 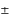 1). 1).
We observe that there are just 24 sets of coordinates, with eight lying in each coordinate plane.
 Space packing Space packing
An interesting property of the truncated octahedron is that these polyhedra pack together to fill space, forming a 3-dimensional space tessellation.
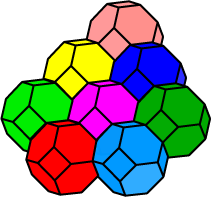 Explore ... Click on the tessellation at right to fade the figure. Now click on the truncated octahedron below, hold the mouse down, and drag the solid across to the space tessellation at right. Try a number of different positions where you think it will fit in the packing – some of the illustrated solids, and some new ones. Explore ... Click on the tessellation at right to fade the figure. Now click on the truncated octahedron below, hold the mouse down, and drag the solid across to the space tessellation at right. Try a number of different positions where you think it will fit in the packing – some of the illustrated solids, and some new ones.
Click here to restore the tessellation figure.
This type of 3-dimensional tessellation is sometimes called an Andreini tesselation: it is a 3-dimensional analogue of the planar semi-regular tesellations. There are in fact 28 Andreini tessellations. They are named in honour of the man who studied and enumerated these tessellations around 1905. All 28 tessellations are found in crystal arrangements. A list of these tessellations can be found in the Wikipedia reference below.
 References References
Wikipedia : http://en.wikipedia.org/wiki/Truncated_octahedron
MathWorld : http://mathworld.wolfram.com/TruncatedOctahedron.html
 Construction : Wenninger, M. J., Polyhedron models, Cambridge (1971). Construction : Wenninger, M. J., Polyhedron models, Cambridge (1971).
Space tessellations : http://en.wikipedia.org/wiki/Andreini_tessellation
It looks as though the total angle defect is always 720° = 4 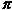 .
In fact this is not quite correct, as we shall see below.
|


 Of course we obtain the truncated octahedron by carefully cutting off (or truncating) the vertices of a regular octahedron. We start with a regular octahedron, and simply trisect each edge into three equal parts. Joining these trisection points gives rise to the squares and regular hexagonal faces of the truncated octahedron. Notice that it is the requirement for regular hexagons that controls the choice of points here.
Of course we obtain the truncated octahedron by carefully cutting off (or truncating) the vertices of a regular octahedron. We start with a regular octahedron, and simply trisect each edge into three equal parts. Joining these trisection points gives rise to the squares and regular hexagonal faces of the truncated octahedron. Notice that it is the requirement for regular hexagons that controls the choice of points here.

