Integrals are extremely important in the study of functions of a complex variable. The theory is elegant, and the proofs generally simple. The theory is put to much good use in applied mathematics.
We shall study line integrals of f(z). In order to do this we shall need some preliminary definitions.
Let F(t) = U(t) +iV(t) (a 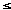 t t 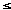 b) where U,V are real-valued, piecewise-continuous functions of t on [a, b], i.e. continuous except for at most a finite number of jumps. The definite integral of F on the interval a b) where U,V are real-valued, piecewise-continuous functions of t on [a, b], i.e. continuous except for at most a finite number of jumps. The definite integral of F on the interval a 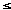 t t 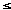 b is now defined by: b is now defined by:
Definition 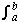 F(t) dt = F(t) dt = 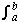 U(t) dt + i U(t) dt + i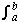 V(t) dt. V(t) dt.
|
|
Properties of the Definite Integral
|
 |
 |
Examples

Contour Simple closed contour
|
Definition For a smooth arc, the length exists and is given by
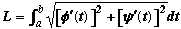 , providing a , providing a 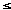 b. b.
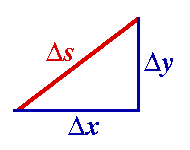 Now, where does this strange formula come from? From Pythagoras' Theorem, the length Now, where does this strange formula come from? From Pythagoras' Theorem, the length  s of a small portion of the arc is given by s of a small portion of the arc is given by
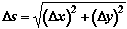 . .
Dividing through by 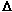 t gives t gives
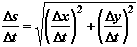 . .
Integrating this expression with respect to t gives the required result.
Note It can be shown that this formula is independent of the choice of parameter used.
Here, 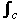 f(z) dz is a line integral, or contour integral. f(z) dz is a line integral, or contour integral.
Note that the line integral exists because the integrand on right is sectionally continuous.
|
|
Expanding the Line Integral
|
 |
 |
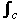 f(z) dz = f(z) dz = 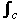 (u dx – v dy) + i (u dx – v dy) + i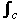 (u dy + v dx). (u dy + v dx).
Note In summary, 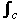 f(z) dz = f(z) dz = 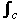 (u + iv)(dx + i dy). (u + iv)(dx + i dy).
Thus we have expressed the complex line integral in terms of two real line integrals.
|
|
Properties of the Line Integral
|
 |
 |
Proof We use Property 5 of the Definite Integral:
|
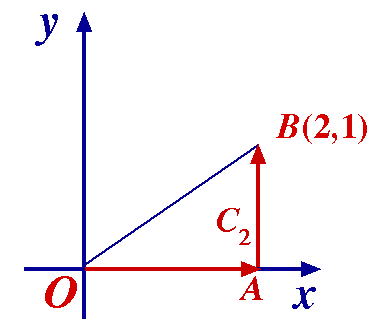
Find I1 = 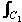 z2 dz, where C1 is the illustrated path OB. z2 dz, where C1 is the illustrated path OB.
|
 Line OB has equation x = 2y. Taking y as parameter we obtain the set of points (2y, y) (0 Line OB has equation x = 2y. Taking y as parameter we obtain the set of points (2y, y) (0  y y  1). 1).
Now, z2 is continuous and on C1,
z2 = (x2 – y2) + 2ixy = 3y2 + 4y2i ,
dz = dx + i dy = (2 + i) dy
[strictly (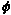 '(y) + i '(y) + i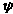 '(y)) dy]. '(y)) dy].
Hence
I1 = 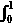 (3y2 + 4y2i)(2 + i)dy = (3 + 4i)(2 + i) (3y2 + 4y2i)(2 + i)dy = (3 + 4i)(2 + i) 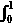 y2 dy = 1/3.(2 + 11i). y2 dy = 1/3.(2 + 11i).
|
Find I2 = 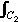 z2 dz, where C2 is the illustrated path OAB. z2 dz, where C2 is the illustrated path OAB.
|
Now
I2 =  OA z2 dz + OA z2 dz +  AB z2 dz AB z2 dz
= 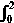 x2 dx + x2 dx + 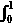 [(4 – y2) + 4iy] i dy [(4 – y2) + 4iy] i dy
= 8/3 + [4 – 1/3 + 2i] = 1/3(2 + 11i).
|
|
Some Interesting Questions
|
 |
 |
Question 1 We see that in the previous examples, the integral from O to B is the same for both contours. Is this a coincidence? Or does it always happen? If it doesn't always happen, when does it?
We can express this in a different way. We see that
So we ask: Is the integral around a closed contour always zero?
Question 2 We observe that if we forget the contour altogether, and simply integrate, then we obtain:
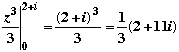 , again! , again!
Does this always happen? This would say that 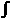 C f is independent of the contour C. C f is independent of the contour C.
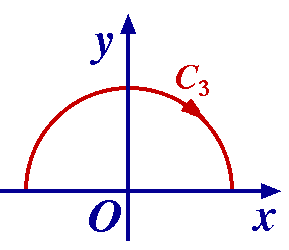
Now C3 is the contour of points
|
Find I4 =   dz, where the contour C4 is shown in red. dz, where the contour C4 is shown in red.
|
|
Without evaluating the integral, find an upper bound for | dz/z4 | on the given contour C5. dz/z4 | on the given contour C5.
|
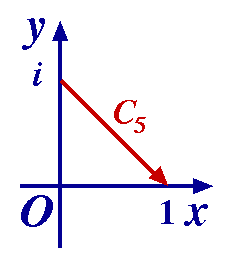 We make use of Property 5: We make use of Property 5:
|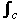 f(z)dz | f(z)dz | 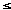 ML. ML.
In this case, the length L = 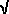 2 . 2 .
Also, the contour C has equation y = 1 – x (0 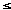 x x 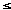 1). 1).
Therefore for z on C
| z4 | = (x2 + y2)2 = [ x2 + (1 – x)2 ]2 = [2x2 – 2x + 1]2.
That is, | z4 | = [2(x – 1/2)2 + 1/2]2 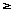 1/4. 1/4.
(In retrospect, this is obvious from the figure! Why?)
Hence | 1/z4 | 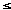 4 and | I | 4 and | I | 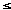 4 4 2 . 2 .
Let R be a closed region in the real plane made up of a closed contour C and all interior points.
If P(x, y), Q(x, y) are real continuous functions over R and have continuous first order partial derivatives, then Green’s Theorem says: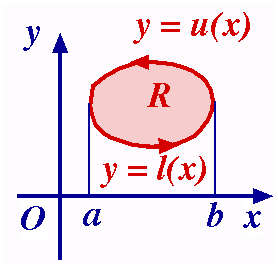
where C is described in the anti-clockwise direction.
Outline Proof
 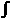 Py dxdy = Py dxdy = 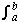 [ [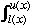 Py dy] dx Py dy] dx
= 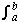 [ P(x, u(x)) – P(x, l(x)) ] dx [ P(x, u(x)) – P(x, l(x)) ] dx
= –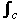 P dx etc. P dx etc.
Now consider a function f(z) = u(x, y) + iv(x, y) which is analytic at all points within and on the closed contour C, and is such that f '(z) is continuous there.
We show that 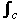 f(z) dz = 0. f(z) dz = 0.
The given conditions tell us that u, v and their first order partial derivatives are continuous. Now
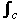 f(z) dz = f(z) dz = 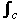 (u dx – v dy) + i (u dx – v dy) + i 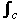 (u dy + v dx) (u dy + v dx)
= – 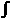 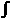 R (vx + uy) dxdy + i R (vx + uy) dxdy + i 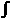 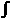 R (ux – vy) dxdy R (ux – vy) dxdy
= 0, using Green's Theorem and the Cauchy-Riemann equations.
This result was discovered by Cauchy.
|
|
Examples and the Cauchy-Goursat Theorem
|
 |
 |
As a consequence of Cauchy's Theorem we have the following:
Goursat showed that Cauchy’s condition ‘f '(z) is continuous’ can be omitted. This discovery is important, because from it we can deduce that all derivatives of analytic functions are also analytic. But, proving this stronger result takes much more effort!
Theorem 5.1 (Cauchy-Goursat Theorem) If a function f is analytic at all points interior to and on a closed contour C, then 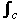 f(z) dz = 0. f(z) dz = 0.
|
|
Cauchy-Goursat Theorem, Example I
|
 |
 |
|
Find 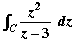 where the contour is the unit circle | z | = 1. where the contour is the unit circle | z | = 1.
|
Now the integrand z2/(z–3) is analytic everywhere except at the point z = 3. This point lies outside the circular disk | z |  1. Hence by the Cauchy-Goursat Theorem 1. Hence by the Cauchy-Goursat Theorem
Most of the useful applications of the Cauchy-Goursat Theorem are as yet
beyond us, but the next example gives us a glimpse of what can be done.
|
|
Cauchy-Goursat Theorem, Example II
|
 |
 |
|
Assuming Laplace’s Integral: 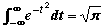 show that show that
|
[We note that Laplace's integral can be evaluated by writing
since the integrand is even.
Let f be analytic in D and z0, z 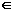 D. Then for contours C1, C2 lying in D, joining points z0, z, and being traversed from z0 to z, D. Then for contours C1, C2 lying in D, joining points z0, z, and being traversed from z0 to z,
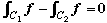 by the Cauchy-Goursat Theorem. by the Cauchy-Goursat Theorem.
Theorem 5.2 (‘Primitive’ Theorem) For all such paths in the domain D
has the same value, and F'(z) = f(z).
Note This will allow us to evaluate some line integrals by straight integration. We shall see that the name of the theorem comes from the fact that the function F satisfying F'(z) = f(z) is called a primitive of f.
|
|
Proof of the ‘Primitive’ Theorem
|
 |
 |
Proof Let z + 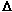 z be a point in D. Then z be a point in D. Then
F(z + 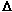 z) – F(z) = z) – F(z) = 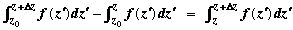 , ,
where since 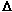 z is very small, we may take the path from z to z + z is very small, we may take the path from z to z + 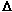 z to be a line segment. z to be a line segment.
Now clearly on the segment, 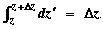 So So
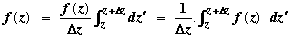 . .
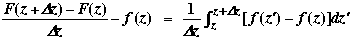
[Continued]
|
|
Proof of the ‘Primitive’ Theorem (Continued)
|
 |
 |
Now f is continuous at z. Hence for all  > 0, there exists > 0, there exists 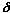 > 0: > 0:
Hence, when | 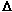 z | < z | < 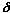 , ,
(using Property 5).
That is,
and F(z) exists at each point of D, and F'(z) = f(z).
|
|
Notes on the ‘Primitive’ Theorem
|
 |
 |
We say that F is an indefinite integral or primitive (anti-derivative) of f and write F(z) = 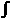 f(z) dz. f(z) dz.
That is, F is an analytic function whose derivative is f(z).
Since
we can use this as a means of evaluating line integrals.
(All paths here are assumed to be in the domain D.)
|