8. POLE AND POLAR
|
Let P and Q be inverse points with respect to a given circle. We draw through Q a line p perpendicular to line PQ. Then p is called the polar of the point P. The point P is called the pole of the line p.
Proof Let TT' meet AB in Q. We show that Q is in fact the inverse of P. Since PT is a tangent and TT' OT / OP = OQ / OT. So If P lies on the circle, the definition tells us that the polar p of P is the tangent at P. |
|
Proof To show that Now, OP.OQ = a2 = OU2 (since P, Q are inverse points), so OU / OP = OQ / OU. It follows that triangles UOP, QOU are similar, since they have a common angle at O. Hence UP / UO = QU / QO (#). We can argue similarly with triangles VOP, VOQ to obtain VP / VO = QV / QO (‡). Noting that UO = VO, dividing equations (#) and (‡) gives our required result (*). Thus p is an angle bisector of |
You might think we have already established this with Theorem 8.1 above, and this is true in the case where the line PR intersects the circle. But what if PR does not intersect the circle? In the diagram, let S be the inverse of R. Then It follows that points P, Q, R, S are concyclic. Since In other words, PS is the line through S perpendicular to line ORS – the polar of R. It follows that P lies on the polar r of R. |
Extensions 1. Show that if the polar of P with respect to a circle meets the polar of Q in R, then the polar of R is PQ. |
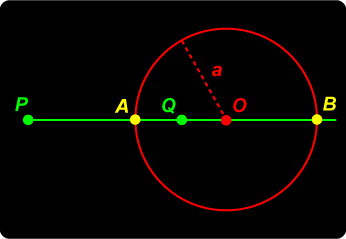 Inverse Points
Inverse Points 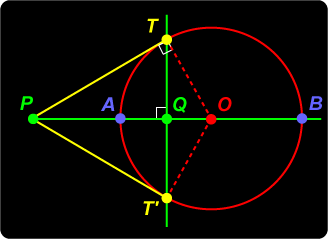 Pole and Polar
Pole and Polar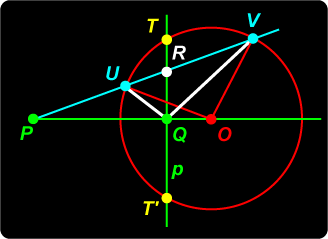 Polar Locus
Polar Locus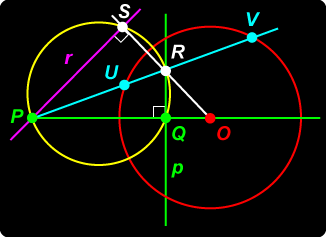 Reciprocal Property
Reciprocal Property