9. THE CYCLIC QUADRANGLE
|
| Surprising? We have previously thought about harmonic sets (ranges) applying to points lying on circles. These results actually apply more generally to conics. We can define a conic as the locus of points which satisfy a general second degree equation: ax2 + by2 + 2fy + 2gx + 2hxy + c = 0. In the case of the quadrangle, we may think of the four points A, B, C, D lying on a pair of opposite sides – a line pair. These form a degenerate conic, since they will have equation (lx + my + n).(px + qy + r) = 0 an equation of the second degree. Hence it is not really surprising to find the harmonic properties occurring here. |
| Quadrilateral The words quadrangle and quadrilateral are easily confused. In projective geometry, quadrangle is defined as in the text. You can think of the name as implying that the points determine the four angles (as in the case of a convex figure). On the other hand, quadrilateral speaks of four lines or edges, which determine six points. If you draw the figure, there are three extra lines dtermined by these points: the sides of a (different) diagonal triangle. Quadrangle and quadrilateral are said to be dual concepts. Not all authors are careful to distinguish these terms. |
Suppose now that the vertices A, B, C, D of the quadrangle lie on a circle. Let |
Extensions 1 Given our quadrangle as usual, show that the two sides of the diagonal triangle meeting in X harmonically separate the quadrangle sides AD and BC meeting in that point. |
P
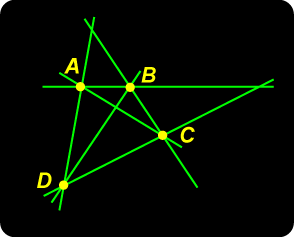 Quadrangle – No Circle!
Quadrangle – No Circle! 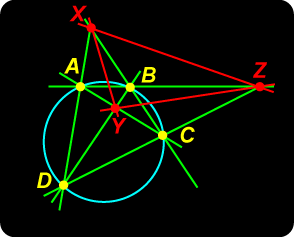 Cyclic Quadrangle
Cyclic Quadrangle