|
7. UNEQUAL SQUARES |
|
|
|
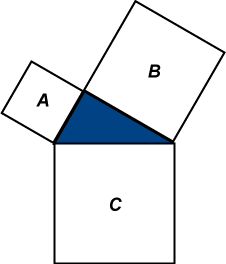
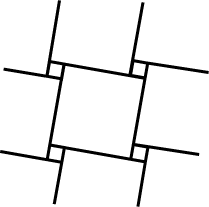
 Problem S3. Dissect a square into 2 equal squares. Problem S3. Dissect a square into 2 equal squares.This problem is trivial (try it!). Click the figure at right to see how this works. This is a special case of one of the prettiest dissection proofs of Pythagoras’s theorem, due to Henry Perigal. (Who was he?) In the figure at left, we dissect squares A and B to form the large square C. You might try this. As a hint, divide up square B by drawing vertical and horizontal segments through the centre. You should obtain this dissection. Now try covering square C by dragging the pieces. Can we obtain the Perigal dissection by using tessellations? Consider the tessellation T below, made up of a combination of (replicas of) squares A and B of edge length a, b respectively. We superimpose a square tessellation of squares of side |
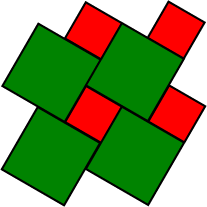 Notice that the choice of big square side length guarantees (using areas) that a red square and a green square together make up a big square. Now move the square tessellation around to obtain a variety of asymmetric Perigal dissections. You can check the corresponding green pieces. Notice that the choice of big square side length guarantees (using areas) that a red square and a green square together make up a big square. Now move the square tessellation around to obtain a variety of asymmetric Perigal dissections. You can check the corresponding green pieces.Problem S4. Use two different tessellations of type T to dissect two squares into two different squares. We introduce this new tessellation T2. Place T2 so that the small squares are concentric with the green squares. The two generating squares in each of T and T2 have the same total area. You should now be able to see a 6-piece dissection of one pair to the other. [Also, can you find another interesting position of T2?] |
|