|
 1. Binomial coefficients 1. Binomial coefficients2. Pascal's Triangle 3. The Sierpinski Sieve
|
| Binomial coefficients
A common task in algebra is to take the sum The product is calculated by multiplying each term in the first factor by each term in the second, adding the results, to give: 1. We can extend this idea to other powers. Try working out the expansion (a + 1)3 by multiplying each term of a2 + 2a + 1 by a and by 1 and then adding all the results. Then work out the expansion for (a+1)4. If the process is continued, we get |
The binomial coefficients are the coefficients of the powers of a in these expansions.
2. Can you see a pattern developing here? Can you make a conjecture about the expression for (a + 1)6? How many terms will it have? What will the coefficients be? We draw up a table of the coefficients of these expressions. Let us include
|
||||
| Pascal's triangle
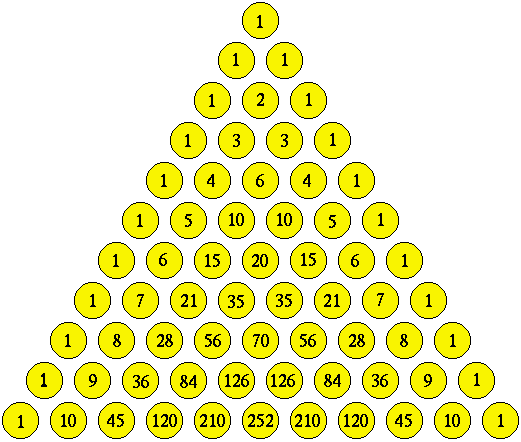
The triangle of binomial coefficients is called Pascal’s triangle. A larger part of Pascal’s triangle is shown in the picture below. It grows downwards indefinitely.
|
3. How is each each number in the triangle related to the numbers immediately above it? What is the next row of the triangle? The name ‘Pascal’s triangle’ might suggest that the triangle originated with the French mathematician, Blaise Pascal (1623-1662). In fact, he did extensive work with the triangle, but it was known to the Chinese centuries before his time. Pascal’s triangle is a source of many interesting patterns. 4. What would happen in the picture if you shaded black all circles containg odd numbers? How do you think the pattern would develop as you move further down the triangle? |
| The Sierpinski Sieve
The pattern of odd numbers in Pascal’s triangle is closely related to a fractal called the Sierpinski Sieve. The construction of a Sierpinski Sieve is easy to describe. The level 0 sieve is just a triangle. Join the midpoints of each side, dividing the triangle into four smaller triangles with the same shape. Remove the central triangle. This gives the level 1 sieve, shown here. If the process is repeated with the three remaining triangles, we get the level 2 sieve, and so on. We shortly give a program that will display a Sierpinski Sieve of size 200 and level 5. The position of the left hand vertex of the sieve on the screen is also specified by the coordinates -100, -90. |
You will see that the program contains
5. Surprisingly, with this program, sieves of high level (more than about 6) vanish. Can you see why? The result of the area calculation (see investigation 10 below) may give you a clue. It is better then to construct the sieve by drawing, rather than removing points. A completely different method for drawing the Sierpinski sieve is given in Section 10. |
|
The Logo program
Here is the Sieve program and the resulting Level 5 Sierpinski Sieve.
|
 |
||
| Further investigations
6. Add the numbers in each row of Pascal’s triangle, and write down the totals. What kind of sequence do you get? Relate this to the definition of the binomial coefficients. 7. What other patterns can you find in Pascal’s triangle? On separate (large!) copies of the triangle, shade all the numbers that are exactly divisible by 3, 4, 5 etc. You will be amazed at the resulting patterns. |
8. There is a formula for calculating any number in Pascal’s triangle without having to calculate the numbers above it. For the kth number in the nth row, the formula is:
Use the formula to calculate the middle (16th) number in row 31. Is it coloured black or white? 9. Each number in Pascal’s triangle is in fact the number of different paths by which it can be reached from the top of the triangle, moving downwards at each step. Verify this fact for the fourth row. 10. What is the perimeter of the Sierpinski sieve? What is its area? Use the same techniques as in previous chapters. The result of the area calculation may surprise you. |



 A further refinement is to have several colours or patterns, and shade numbers depending on their remainder when divided by a given number.
A further refinement is to have several colours or patterns, and shade numbers depending on their remainder when divided by a given number.