 The French priest Marin Mersenne (1588 –1648) played an important role in 17th century number theory and also more general mathematics. Scholars inquisitive about mathematics or stumped by a difficult problem would often write to Mersenne who could direct them to a likely authority, if he didn’t know the answer himself. Today Mersenne’s name is mainly associated with numbers of the form 2n – 1; that is, numbers one less than a power of 2. To honour Mersenne these are called Mersenne numbers. It is clear that all such numbers are odd but more importantly some of them are prime; as is the case with 213466917 – 1.
The French priest Marin Mersenne (1588 –1648) played an important role in 17th century number theory and also more general mathematics. Scholars inquisitive about mathematics or stumped by a difficult problem would often write to Mersenne who could direct them to a likely authority, if he didn’t know the answer himself. Today Mersenne’s name is mainly associated with numbers of the form 2n – 1; that is, numbers one less than a power of 2. To honour Mersenne these are called Mersenne numbers. It is clear that all such numbers are odd but more importantly some of them are prime; as is the case with 213466917 – 1.
Mersenne immediately understood
that if n is composite then 2n – 1 must also be composite. For example take n = 33, then
233 – 1 = 8,589,934,591 = 7 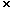 1,227,133,513
1,227,133,513
is not a prime. However when
n is prime, the situation becomes less clear. Letting p = 2, 3, 5, and 7 yields the “Mersenne primes”
22 – 1 = 3, 23 – 1 = 7, 25 – 1 = 31, and 27 – 1 = 127
respectively. But if we take p = 11 as the exponent we get 211 – 1 = 2047 = 23 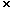 89. Mersenne was also fully aware that a prime p was not enough to guarantee 2p – 1 to also be prime. In fact he made the following assertion in his book Cognitata Physica-Mathematica:
89. Mersenne was also fully aware that a prime p was not enough to guarantee 2p – 1 to also be prime. In fact he made the following assertion in his book Cognitata Physica-Mathematica:
“The only primes between 2 and 257 for which 2p – 1 is prime
are p = 2, 3, 5, 7, 9, 11, 13, 17, 19, 31, 67, 127 and 257.”
Unfortunately Mersenne missed the fact that the numbers 261 – 1, 289 – 1 and 2107 – 1 are in fact prime. But conversely 267 – 1 and 2257 – 1 turned out not to be prime at all. We can forgive Mersenne for these errors as he lived in the pre-computer age. The case of 267 – 1 was proved by Edouard Lucas (1842 – 1891) in 1876 who used an argument which did not explicitly yield any of the factors. It was not until the following century that Frank Nelson Cole did find its factors.
 The French priest Marin Mersenne
The French priest Marin Mersenne  The French priest Marin Mersenne
The French priest Marin Mersenne ![]()