|
2. LATTICE POLYGONS AND POLYHEDRA A lattice polygon (lattice polyhedron) is a polygon (polyhedron) for which every vertex is a lattice point. Here are some examples:
A (general) set is convex if for any two points of the set, the line segment joining those two points lies within the set. In the case of polygons, a polygon is convex if it has no re-entrant angles. At right is an example of a convex set: It is obviously possible to have a non-convex set:A polygon is simple if it is not self-intersecting. It is easy to produce a non-simple (lattice) polygon: Most of the sets we study will be convex and simple. There are some very special parallelograms associated with a lattice. These have lattice points as vertices, and no other lattice points on their edges or in their interiors.
|
|||
|
You probably found that all these lattice paralellograms have the same area – in fact, equal to 1 for the integer lattice. Any such parallelogram is called a fundamental parallelogram of the lattice. How to establish the area property? (1) Coxeter [C] associates any particular fundamental parallelogram with a vertex lattice point. Then inside any sufficiently large circle, the number of lattice points is equal to the number of replicas of the fundamental parallelogram, apart from an insignificant number of mutilated regions around the circumference of the circle. Thus every fundamental parallelogram has the same area. In this argument, you may be unhappy about the term ‘insignificant number’, seeing that this number could be quite large. The point is that the number of replicas is a number like N2, while the number of mutilated regions is more like the much smaller N, since the circumference is a linear quantity.
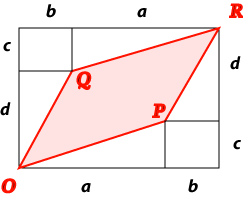
A = (a + b)(c + d) – 2bc – bd – ac = ad – bc. In general, depending on the way we choose our vectors, this may be negative. So A = | ad – bc |. Now all the points of the lattice L' determined by OP and OQ are given by
where x, y are arbitrary integers. But now by the IU Theorem, a necessary and sufficient condition that L' be identical with the integer lattice L is that | ad – bc | = 1. Thus A = 1. We have proved: Fundamental Parallelogram Theorem All fundamental parallelograms of a given lattice have the same area. In the case of the integer lattice, this area is 1. In the case of a general lattice L, the area of a fundamental parallelogram is denoted by d(L) and called the lattice determinant. Any lattice triangle which has its vertices at lattice points, but no interior lattice points and no other lattice boundary points, is called a primitive triangle. Any such triangle occurs as half of some fundamental parallelogram. Hence any primitive triangle in the integer lattice has area 1/2. Primitive Triangle Theorem All primitive triangles in a given lattice have the same area. In the case of the integer lattice, this area is 1/2. Further result (1) The Fundamental Paralellogram Theorem generalizes to higher dimensions in the obvious way, with a fundamental parallelopiped in 3 dimensions, and a fundamental parallelotope in higher dimensions. The lattice determinant also occurs and has useful application in higher dimensions. Primitive triangles seem to have no useful analogue in higher dimensions. [C] Coxeter, H. S. M., Introduction to Geometry, Wiley (Edition 2 1969) page 53. [HW] Hardy, G. H., Wright, E. M., An introduction to the theory of numbers, Oxford (Edition 4 1960) page 28. |
|||||
 Experiments with lattice polygons can be easily carried out with the help of a geoboard. This is a board with a grid of nails (golf tees) around which a rubber band can be wound.
Experiments with lattice polygons can be easily carried out with the help of a geoboard. This is a board with a grid of nails (golf tees) around which a rubber band can be wound.