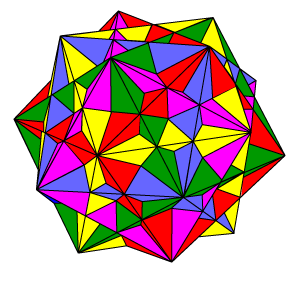
FIVE CUBES COMPOUND

    Cubes and the dodecahedron

We have already seen how it is possible to inscribe a cube inside a dodecahedron, using eight of the vertices of the dodecahedron. In fact it is possible to inscribe five different cubes to form a the complicated but pretty compound shown. Five cubes have 40 vertices; a dodecahedron has 20 vertices. Hence using the symmetry of the compound, each vertex of the dodecahedron occurs as the vertex of two of the cubes. Because of the complexity of this compound, it is better to simply enjoy it, rather than analyzing it too deeply. However, we note that the edges of the cubes lie by fives on the faces of the underlying dodecahedron forming regular pentagrams. This means that each edge is divided by two other edges in golden section.    View this structure.

We can break the model down into its five component cubes.

Another way of viewing the compound is to remove the cubes one by one:     

  The intersection of the cubes

We can define a unique rhombus with each of the faces of each of the cubes. For example, consider the blue cube in the adjacent figure, and the upward/left facing face. As noted above, faces of the other four cubes intersect the edges of the blue cube face in the face vertices and at pairs of points on each face edge (which in fact divide the edge in the golden ratio). If we draw in the lines where the faces meet (vertex to furthest opposite golden point), a rhombus is determined. Since the five cubes each have six faces, there are 30 such rhombuses. These form a polyhedron known as a rhombic tricontahedron, (below) which is the solid intersection of points common to all the five cubes.

Click the figure at right to restore the original.

  Making the model

This is one of the more difficult polyhedral models you may try to make. A cut-out model is available through Tarquin publications (see references below). Alternatively, detailed nets are available on the site by Gijs Korthals Altes, or here. Otherwise, you can make your own model directly using the guide given in Cundy and Rollett or Math World (both below). You will need a lot of perseverance! There seems little pint in reproducing the complicated nets here.

For some reason, this model appears to be omitted from Wenninger’s Polyhedral Models (at least in my edition).



  Playing with the applet

It is profitable to spend some time playing with the applet, and enjoying this beautiful compound polyhedron. Use the applet to check out the following statements:

• The compound places a pentagram in each dodecahedral face.

• The compound places an equilateral triangle about each dodecahedral vertex.

• The dodecahedral outline is an irregular hexagon precisely when the viewer looks directly at a cube face.

• Each triangular dimple formed by three of the cubes contains a hexagonal ‘floret’ formed by the two remaining cubes having a common vertex.



  Vertex coordinates

When we looked at the dodecahedron, we discovered that we can take as coordinates for the 20 vertices:

(1, 1, 1),   (0, –1, ),  (, 0, –1),  and  (–1, , 0).

These then will form the vertices of the five cubes, but in which order?

Obviously one cube can be given the coordinates (1, 1, 1).

    • (a) Try to find the coordinates of the remaining four cubes. To help, you might ask: what is the side length of each cube? We also know that each of the vertices of the given cube is a vertex of another cube as well. So, why not start by looking at (1, 1, 1)? Remember that 2 = + 1, and so –1 = – 1.
        (b) As you do your calculations, watch out for some interesting facts about the cubes which will help simplify your work.

Now check your answers ...

































  When we looked at the dodecahedron, we discovered that we can take as coordinates for the 20 vertices:

(1, 1, 1),   (0, –1, ),  (, 0, –1),  and  (–1, , 0).

These then will form the vertices of the five cubes, but in which order?

Obviously one cube can be given the coordinates (1, 1, 1).    

• (a)  Try to find the coordinates of the remaining four cubes. To help, you might ask: are the cubes symmetric about the origin? what is the side length of each cube?  We also know that each of the vertices of the given cube is a vertex of another cube as well. So, why not start by looking at (1, 1, 1)? Remember that 2 = + 1, and so  –1 = – 1.
   (b)  As you do your calculations, watch out for some interesting facts about the cubes which will help simplify your work.

The given cube is symmetric about the origin. Since the cubes have side length 2, the major diagonals of each cube will have length 12.

Noting that the distance between (1, 1, 1) and (–1, –1, –1) is also 12, it seems a fair bet that each cube is symmetric about the origin, and that the cubes occur in pairs having a pair of diagonally opposite vertices in common.

It is a simple matter of trial and error to determine that vertex (1, 1, 1) is distant 2 from the dodecahedral vertices (0, – –1, ), (, 0, – –1 ) and (– –1, , 0) (and only from these vertices). For example, the distance s between the points (1, 1, 1) and (0, – –1, ) is given by

s2 = 1 + (1 + –1)2 + (1 – )2 = 1 + (1 + 2 –1 + –2) + (1 – 2 + 2) = 2 – 2 + 2 2 = 4.

It follows that vertices (0, –1, –), (–, 0, –1 ) and ( –1, –, 0) are distant 2 from (–1, –1, –1), and we now have the required eight vertices of the second cube:

(1, 1, 1), (0, – –1, ), (, 0, – –1 ) and (– –1, , 0).

If you feel unsure about our assertions, you can check the distances between each pair of vertices of the cube. Similar calculations now give the vertex sets of the remaining three cubes:

(–1, 1, 1), (0, – –1, ), (–, 0, – –1 ) and ( –1, , 0),

(1, –1, 1), (0, –1, ), (, 0, – –1 ) and (– –1, –, 0).

(1, 1, –1), (0, – –1, –), (, 0, –1 ) and (– –1, , 0).

In fact, the five cubes are given by the initial cube, and the five rotations through 2/5, 4/5, 6/5 and 8/5 about the axis (1, , 0).

There are of course other vertices occurring within this compound; for example the two golden section points on each edge of each cube.
  
   We obtain the above results by looking straight down on the model with a     vertex of

   (a) the octahedron and

   (b) a vertex of the cube closest to the eye.

    V          E         F       V – E + F  
62
180
120
2 

Obtaining these numbers is getting a little more tricky.
For V we obtain 20 + 12 for the vertices of the dodecahedron and the icosahedron, + 30 for the midpoints of one set of edges. For E counting twice the number of edges of each polyhedron gives 60 + 60, and then add 60 for three further edges on each icosahedral face. For F we obtain 120: six triangular faces for each of the 20 icosahedral faces.