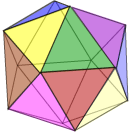
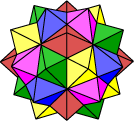
59 STELLATIONS OF THE ICOSAHEDRON :
EXAMPLES AND THEORY
 The icosahedron case The icosahedron case
We have looked at the stellations of the octahedron and dodecahedron. Now we come to the more interesting case of the icosahedron.
• Let’s begin by just playing with the applet below. Notice the great variety of shapes and structures, yet all bearing the characteristics of the icosahedron or the dual dodecahedron. Play with the different controls to understand their functions. Notice how it is possible to view the stellation diagram for each polyhedron.
 Some old friends Some old friends
Some of the polyhedra we have already studied actually occur as stellations of the icosahedron.
• Use the applet above to browse through the various stellations to find the stellation number for each of the following.
Enter the stellation number in the space provided.
Check your answers ...

 Some old friends Some old friends
Some of the polyhedra we have already studied actually occur as stellations of the icosahedron.
• Use the applet above to browse through the various stellations to find the stellation number for each of the following.
Enter the stellation number in the space provided.
| the icosahedron : |
stellation number |
0 |
| the compound of five octahedra : |
stellation number |
2 |
| the compound of five tetrahedra : |
stellation number |
46 |
| the compound of ten tetrahedra : |
stellation number |
21 |
| the great icosahedron : |
stellation number |
6 |
The numbers are given above. You can check with the diagrams below, taken from our previous work.
Clicking on a label will take you to our previous work on this polyhedron.
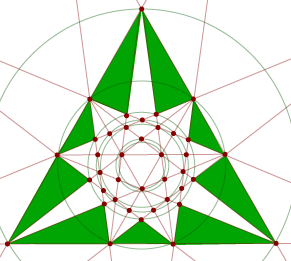
  Stellation diagrams for the icosahedron Stellation diagrams for the icosahedron
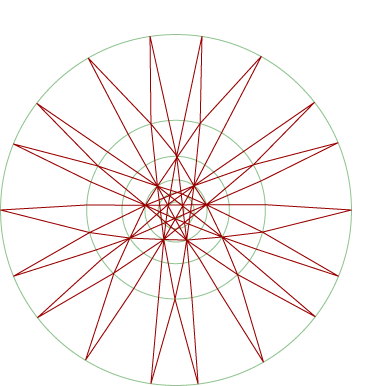
We can create a stellation diagram for the icosahedron, just as we did for the dodecahedron. It is shown at right. (We have distorted the spikes a little to keep the diagram a reasonable size.) In order to see better the structure near the centre, it is helpful to just look at this part of the diagram:
In the close up view, the adjacent converging arrows indicate lines meeting on the outer circle.
The interior triangle is a face of the basic icosahedron. By the symmetry of the stellated figure, a given particular stellation diagram with shading for the visible faces, will occur for each face plane of the interior icosahedron.
There are clearly an immense number of possibilities here, corresponding to various colourings of the stellation diagram.
Computer scientist and mathematician Dr J. C. P. (Jeff) Miller of Cambridge came up with a set of rules for deciding which stellations of the icosahedron should be counted as valid. They are as follows:
1. The faces must lie in twenty planes, viz., the bounding planes of the regular icosahedron.
2. All parts composing the faces must be the same in each plane, although they may be quite disconnected.
(Rules 1 and 2 are just the basic setting up of the stellation diagrams.)
3. The parts included in any one plane must have three-fold symmetry, with or without reflection. This secures icosahedral symmetry for the whole solid.
4. The parts included in any plane must all be ‘accessible’ in the completed solid.
(This means they must be on the ‘outside’. In certain cases we should require models of enormous size in order to see all the ‘outside’. With a model of ordinary size, some parts of the ‘outside’ could only be explored by a crawling insect or a fine medical probe!)
5. We exclude from consideration cases where the parts can be divided into two sets, each giving a solid with as much symmetry as the whole figure. But we allow the combination of an enantiomorphous pair (a mirror image pair) having no common part. (This actually occurs in just one case.)
It is not really important to know or understand these details unless you wish to do a complete study of these stellations. However, it is worth knowing that some constraints have been put in place. The classic work on the 59 stellations is the book on this topic by H. S. M. Coxeter and others, listed below.
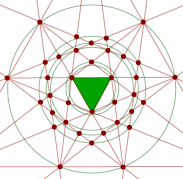
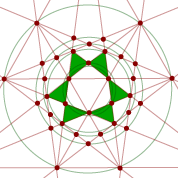
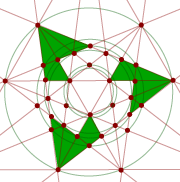
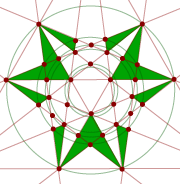
The stellation diagrams for the above five stellations are given below.
 |
 |
 |
 |
|
Icosahedron
|
Compound of 5 octahedra
|
Compound of 5 tetrahedra
|
Compound of 10 tetrahedra
|
British Origami Society : http://www.prospero78.freeserve.co.uk/icosa/icosa.htm
Coxeter, H. S. M., du Val, P., Flather, H.T., and Petrie, J. F., The 59 icosahedra, University of Toronto (1951).
[The classic reference on this topic.]
A newer version of this book can be accessed through Amazon on
http://www.amazon.com/gp/product/1899618325/ref=nosim/002-2157352-7234419?redirect=true&n=283155
Coxeter, H. S. M., Regular Polytopes, Macmillan 2nd Ed. (1963).
Dutch, Steven : http://www.uwgb.edu/dutchs/symmetry/stellate.htm
Wenninger, M. J., Polyhedron Models, Cambridge (1979).
[Note that Wenninger’s numbering differs from that given here.]
Wolfram MathWorld : http://mathworld.wolfram.com/IcosahedronStellations.html

|